 动态储油池计算原理及应用
动态储油池计算原理及应用
基于动力系统的储油池计算,Mackey-Glass system适用于电子实现,Ikeda system适用于光电实现;基于口述数字识别数据集 Free Spoken Digit Dataset (FSDD) (opens new window)完成仿真实验。主要考察内容:
- [x] 实现MG/Ikeda-based的DRC框架
- [x] Lyon耳蜗模型 VS MFCC
# Reservoir Computing
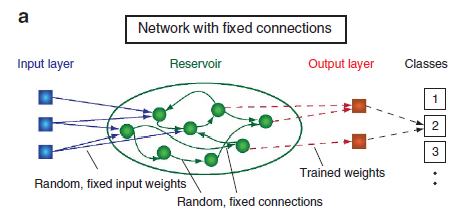
- RC 的主要灵感来源于大脑处理由输入感觉信号激发的瞬时神经元活动的信息生成模式的洞察力。因此,RC 是在模仿神经元网络。
- 传统的 RC 实现通常由三个不同的部分组成: 输入层、存储层和输出层,如图所示。输入层通过固定的随机重量连接将输入信号反馈给储存器。水库通常由大量随机相互连接的非线性节点组成,构成一个递归网络,即具有内部反馈回路的网络。在输入信号的影响下,网络表现出瞬态响应。这些瞬态响应通过单个节点状态的线性加权,并在输出层读出。RC 的目标是对输入信号进行特定的非线性变换或对输入信号进行分类。为了完成它的任务,RC 需要一个训练程序。由于循环网络是众所周知的难以训练,他们没有被广泛使用,直到出现 RC。在 RC 中,这个问题通过保持连接固定来解决。**系统中唯一被训练的部分是输出层权重。**因此,训练并不影响水库本身的动态。作为这个训练过程的结果,系统能够概括,也就是说,处理看不见的输入或将它们归属于以前学过的类。
- RC的三个特征:高维映射,短时记忆(太远的不需要),可复现且对噪声鲁棒。经验表明,当油藏在一个稳定的状态下运行(在没有输入的情况下) ,但离分岔点不太远时,这些要求就得到满足。【如何确定分岔点?】
- 先求和再非线性:$\boldsymbol{x}(k)=f\left(W_{\text {res }}^{\text {res }} \cdot \boldsymbol{x}(k-1)+W_{\text {in }}^{\text {res }} \cdot \boldsymbol{u}(k)+W_{\text {out }}^{\text {res }} \cdot \hat{\boldsymbol{y}}(k-1)+W_{\text {bias }}^{\text {res }}\right)$
# 特征表示
一句话得到特征形状(nChunk, nChannel),
# Lyon's ear model

- 里昂被动耳模型是人类内耳或耳蜗的模型,它描述了人类耳蜗将声音转换为内耳内毛细胞产生的一系列神经棘波的方式。该模型由滤波器组组成,滤波器组与人耳对某些频率的选择性非常相似,随后是一系列半波整流器(HWR)和自适应增益控制器(AGC),它们都对毛细胞响应进行建模。这种形式的预处理在计算上比MFCC前端更密集。在传统处理器上计算所需的时间大约是原来的三到五倍。
- 从本质上讲,耳蜗是非线性滤波器组:由于其刚度的可变性,沿着它的不同位置对具有不同频谱内容的声音都是敏感的。然而,该模型并没有试图从字面上描述耳蜗中的每一个结构,而是将其视为一个“黑匣子”。就像进入耳蜗的声音被转换成神经放电,沿着听觉神经向上进入大脑一样,该模型输出一个与耳蜗中每个点的神经元放电率成比例的向量。
- 耳蜗模型结合了一系列滤波器,这些滤波器利用半波整流器(HWR)重建行进的压力波,以检测信号中的能量,以及自动增益控制(AGC)的几个阶段:这种行为由级联滤波器组模拟。**滤波器的数量取决于信号的采样率、滤波器频带的重叠因子、滤波器的谐振部分的质量以及其他因素。**滤波器越多,模型越准确。
- 该模型产生了听觉神经放电率图,称为耳蜗电图(Cochleagram)。耳蜗图是频谱图的变体,指用于更好地揭示频谱信息的二维时频表示。虽然在粗略的时间尺度上,耳蜗图和频谱图看起来非常相似,除了频率轴的尺度之外,耳蜗图可以保留每个声音分量的更多精细时间尺度结构,例如声门脉冲。
- AGC是用来衰减输入信号的,所有信道都是相互影响的,随着距离呈指数衰减
- Lyon's ear model的获取流程:级联滤波器→半波整流→自动增益控制,级联滤波器包括外中耳滤波器、补偿器、一对极点滤波器、补偿器、一组耳蜗滤波器及对应的补偿器
# MFCC
- MFCC是语音识别领域中非常流行的预处理技术,计算方法如下:(1)使用汉明窗对样本数据进行加窗,并计算FFT;(2)通过所谓的mel-scale2滤波器组计算幅值,并计算这些值的log10;(3)应用余弦变换来降低维数并增强输入的语音特征。结果就是所谓的倒谱。
- MFCC由滤波器提取,滤波器的带宽根据人类对音调的感知相对于非线性频率尺度分布。里昂耳蜗模型基于对人类听觉系统的研究,并对耳蜗或内耳的行为进行建模。
- MFCC表示对数地位于mel频率标度上的频带中的倒谱信息,mel频率是听众判断为彼此距离相等的特定音高范围。MFCC部分基于对听觉感知的理解:对数能量标度匹配耳朵的对数响度感知,mel频率标度基于音调感知。
- MFCC的获取流程:分帧(301, 1103)→加窗(301, 1103)→频域能量谱密度(301, 4069)→对每个频域区间中的能量求和得到${MFCC}_0$(301, 1) →经Mel滤波器过滤,得到Mel尺度下的能量谱(301, 26)→对每一帧取log后进行离散余弦变换(301, 26)→对于前13维乘上升倒谱系数(301, 13),因为只有低频部分有效
# 异同点
MFCC的计算比Lyon快很多,Lyon好慢好慢?
里昂的耳模型比梅尔频率倒谱系数(MFCC)慢,因为它使用了更复杂的处理管道。里昂的耳朵模型基于人类耳朵的生理模型,包括模拟耳朵处理声音的多个处理阶段。这包括模拟内耳对不同频率的反应方式的滤波和压缩操作。与MFCC中使用的处理步骤相比,这些操作的计算量更大,这使得里昂耳模型的计算速度更慢。 此外,与MFCC相比,Lyon’s ear模型通常需要更多的滤波器组,这也导致其处理时间较慢。相比之下,MFCC使用更简单的处理管道,该管道仅包括倒谱系数的计算,因此计算速度更快。总之,里昂耳模型的处理时间较慢是因为其处理管道更复杂,包括多个过滤和压缩阶段,这些阶段旨在模拟人耳。
Lyon与MFCC使用的滤波器组一样吗? 里昂耳模型模拟了听觉系统的外围处理,包括耳蜗滤波,它可以被认为是分离语音信号的不同频率分量的滤波器组。该模型考虑了内耳的非线性和频率依赖性财产,以执行此滤波。 MFCC使用Mel频率滤波器组将语音信号的功率谱转换为Mel频率表示。梅尔频率滤波器组将频率轴分成重叠的三角形滤波器,每个滤波器以不同的梅尔频率为中心,每个滤波器的输出是该频率范围内的对数能量。然后通过采用Mel频率表示的离散余弦变换(DCT)来获得MFCC。
有参考文献是将语音分帧后,MFCC与Lyon具有相同的帧数即可
Lyon是将语音转为神经响应的电信号,MFCC单纯计算信号的能量,所以Lyon的计算步骤比MFCC多很多
Lyon中的级联滤波器保留了从高到低所有频带,但是MFCC只选取了前13个滤波器,只关注低频信息;
# 参考资料
- MFCC算法讲解及实现(matlab)_王延凯的博客的博客-CSDN博客_mfcc (opens new window)
- Lyon's auditory model for Python (opens new window)
- Our Adaptation of Lyon’s Auditory Model for Python | by Sciforce | Sciforce | Medium (opens new window)
- MFCC特征提取教程 - 知乎 (zhihu.com) (opens new window)
# 岭回归(Ridge regression)
岭回归是一种线性回归,旨在通过在损失函数中添加惩罚项来减少模型中多重共线性的影响。该惩罚项与系数大小的平方和成比例,这导致系数向零收缩,从而减少模型的方差。正则化参数(通常用$λ$表示)决定惩罚项的强度,$λ$值越大,收缩越强。岭回归是防止过度拟合和提高模型可解释性的有用工具。
岭回归方程可以表示为:$y=Xβ+ε$,其中$y$是响应变量,$X$是预测因子的设计矩阵,$β$是系数的向量,$ε$是误差项。正则化项被添加到普通最小二乘损失函数中,以形成岭回归目标:
$$L(\beta) = ||y - X \beta||^2 + \lambda ||\beta||^2$$
其中$||.||^2$表示L2范数,$λ$是控制惩罚强度的正则化参数。通过使用优化算法最小化该目标,可以找到系数$β$的最佳值。
TODO: 惩罚因子的作用?
| 来源 | 表达式 |
|---|---|
| Reservoir_Computing_with_a_Single_Dynamical_Node | np.dot(scipy.linalg.pinv(_X) , _Y) |
| Echo-State-Network-with-Intrinsic-Plasticity | W_out = (y * states') / (states * states' + lambda * eye(size(W_hat, 1) + 1)) |
| ipc | XX = np.linalg.pinv(X.dot(X.T)) zhat = x.T.dot(XX).dot(X.dot(Z)) |
常用代码
# 1)
alpha = 0
Wout = np.linalg.inv((x_train_add[:, Two:] @ x_train_add[:, Two:].T) + (alpha * np.identity(x_train_add[:, Two:].T.shape[1]))) @ (x_train_add[:, Two:] @ z_train[Two:])
# 2)
XX = np.linalg.pinv(x_train_add.dot(x_train_add.T))
Wout = XX.dot(x_train_add.dot(z_train))
# 3)
import sklearn.linear_model as linfit
regression = linfit.BayesianRidge(n_iter=3000, tol=1e-8, verbose=True, fit_intercept=False)
regression.fit(x_train_add[:, Two:].T, z_train[Two:])
Wout = regression.coef_
2
3
4
5
6
7
8
9
10
11
12
13
- 这三种写法的结果差不多,3)的效果差一点
# 参考资料
# Dynamic RC
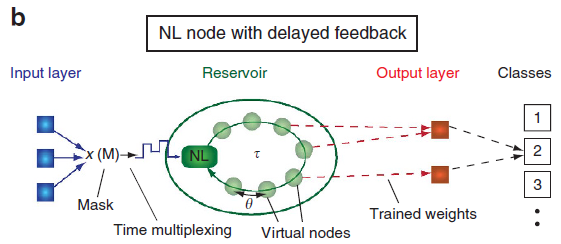
- 一个最简单的可能的时滞系统是由一个单一的非线性节点组成的,它的动力学受到过去它自己输出的时间$\tau$的影响。该系统由两部分组成,一个非线性节点和一个延迟环路,易于实现。
- 数学上来说,连续时间延迟系统的一个重要特征是他们的状态空间会变为无限维。这是因为在时刻$t$的节点状态取决于非线性节点在连续时间段$[t-\tau, t]$的输出。实际操作中,延迟系统的动力还是作为有限维的去处理,可以展现出高维和短时记忆的属性。
- 我们选择 $\theta<T$,$T$ 为非线性节点的特征时间尺度。通过这种选择,虚拟节点的状态将依赖于相邻节点的状态。
- 在每个延迟时间$\tau$中,只处理一个输入信号,也就是说整个输入信号以时间段$\tau$为阶梯函数的区间
- $T$是如何确定的?【😶🌫️至今没能解决】
- 先非线性再求和:$x_{i, k}=\Omega_{n i} x_{n, k-1}+\sum_{j=1}^i \Delta_{j i} f\left(x_{j, k-1}, w_{i n, j} u_k\right)$,其中$\Omega_{n i}=e^{-i \theta}$,$\Delta_{j i}=\left(1-e^{-\theta}\right) e^{-(i-j) \theta}$【感觉推导有点问题】
# 输入:二值掩码
- The masking procedure serves two purposes: sequentializing the input and maximizing the effectively used dimensionality of the system.
- 掩码的作用:1)将输入特征序列化;2)最大限度地使用系统维度;
- In terms of a ‘classical’ reservoir setup, the values of the mask function $M(t)$ correspond to the weights of the connection between the input layer and ther eservoir layer.
- mask的作用类似于输入权重,实现输入样本到高维空间的映射
- 对于语音数字识别任务,掩码由三个值的随机赋值组成: 0.59、0.41和0。前两个值被选中的概率相等,而第三个值更有可能被选中。使用零掩码值意味着某些节点对某些通道不敏感,从而避免对所有通道进行平均。
- Mask的优化:《Constructing optimized binary masks for reservoir computing with delay systems》
# 求解器:the Mackey-Glass system
MG等式的标准形式:
$$\frac{d x}{d t}=\beta \frac{x(t-\tau)}{1+[x(t-\tau)]^p}-\gamma x(t), \quad \text { with } \quad \gamma, \beta, p>0$$
在DRC文章中,该等式形式为
$$\dot{X}(t)=-X(t)+\frac{\eta \cdot[X(t-\tau)+\zeta J(t)]}{1+[X(t-\tau)+\zeta J(t)]^{p}}$$
式中做了如下处理:$\gamma=1, \beta=\eta, \quad \text { and } \quad x(t-\tau) \rightarrow X(t-\tau)+\zeta J(t)$
对于这个方程的数值积分,我们使用隐式中点法 (opens new window):
$X\left( t_n+h \right) =X\left( t_n \right) +h\times f\left( X\left( t_n+\frac{h}{2} \right) \right)$
$=X\left( t_n \right) +h\times \left[ -X\left( t_n+\frac{h}{2} \right) +\frac{\eta \left[ X\left( t_n+\frac{h}{2}-\tau \right) +\zeta J\left( t_n+\frac{h}{2} \right) \right]}{1+\left[ X\left( t_n+\frac{h}{2}-\tau \right) +\zeta J\left( t_n+\frac{h}{2} \right) \right] ^p} \right]$
$=X\left( t_n \right) +h\times \left[ -\frac{X\left( t_n \right) +X\left( t_n+h \right)}{2}+\frac{\eta \left[ X\left( t_n+\frac{h}{2}-\tau \right) +\zeta J\left( t_n+\frac{h}{2} \right) \right]}{1+\left[ X\left( t_n+\frac{h}{2}-\tau \right) +\zeta J\left( t_n+\frac{h}{2} \right) \right] ^p} \right]$
得到迭代式:
$$\left(1+\frac{h}{2}\right) X\left( t_n+h \right)=\left(1-\frac{h}{2}\right) X\left( t_n \right)+ h\frac{\eta\left[X\left(t_{n}+\frac{h}{2}-\tau\right)+\zeta J\left(t_{n}+\frac{h}{2}\right)\right]}{1+\left[X\left(t_{n}+\frac{h}{2}-\tau\right)+\zeta J\left(t_{n}+\frac{h}{2}\right)\right]^{p}}$$
其中 $h$为步长,比$\theta$更加精细。为了完成DDE的积分,我们需要此刻的$X(t)$及其延迟$X(t-\tau)$。对于隐式中点法,我们实际需要$X(t_n)$及$X(t_n+h/2-\tau)$。因此,如果$h/2-\tau$是时间步$h$的整数倍$N$,即$\tau-h/2=Nh$,那么$X(t_n+h/2-\tau)$的值就已经被计算好了,我们可以很快地把它代入到上式。我们选择
$$h=\frac{2 \tau}{2 N+1} \Rightarrow t_n+\frac{h}{2}-\tau=t_n-N h$$
其中,$N$表示用于求解延迟周期$\tau$的总步数,而不是虚拟节点个数
- 反馈增益$η$,输入增益$γ$,延迟时间$τ$,延迟线$θ$,非线性类型(在我们的例子中是MG系统的指数$p$)以及输入掩码的选择
# 代码实现
- 设置一段warm up时间,不输入信号,只是让系统空转,更新虚拟节点输出信号的初始值;
- 对于时间序列预测任务,因为每个样本的timestep是统一的,因此可以所有样本并行放入储油层;对于时间序列分类任务,每个样本的timestep因语音长度而变化,因此只能单个样本投放;
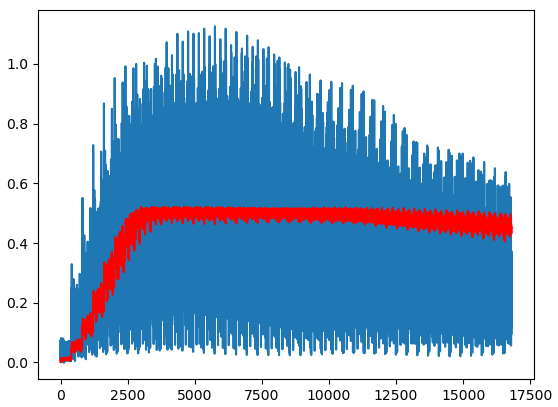
- 红色表示响应,为什么会保持在一条线上?是说明系统能收敛吗?
- 训练时间相当长!
# Lyon耳蜗模型 VS MFCC
我们基于口述数字识别数据集,用DynamicRC做实验对比两个特征:
- 每条语音使用相同数量的帧数,Lyon默认64维,MFCC默认39维;
- 当语音的采样率为16KHz时,Lyon为86维,8KHz时,Lyon为64维;
- Lyon与MFCC得到的数值差很多数量级,因此Lyon模型乘上一个缩放因子,取2e3;【不然识别率会下降30%左右】
- factor[decimation_factor/frame_length]:进入滤波器组的语音采样点数量;【对于8kHz音频,64个采样点表示8ms】
- output:一条语音经过滤波器组后的输出,每条语音尺寸的第二维是一样的,第一维根据语音长度变化
- 该数据集语音集中在0.5s左右,属于短语音;
- 使用了两种音频文件读取工具
wavfile和soundfile,发现两者的输出是不一样的,soundfile输出的是原始语音幅度,wavfile是进行了取整,进行了化简,先前Fit-RNN与Fit-DNN的实验全部用的wavfile,但是整数形式在Lyon算法代码中会报错,所以DRC实验中使用soundfile; - 分帧操作默认为最后一帧进行了补零,且分帧后有加窗操作;
| No. | 特征提取 | factor | output | Acc[%] |
|---|---|---|---|---|
| 1 | 对一整条语音使用原始Lyon算法 | 64 | (42, 64) | 97.8333 |
| 2 | 将分帧融合在Lyon算法中,帧长与No.1对齐,帧不重叠 | 64 | (43, 64) | 98.1667 |
| 3 | 将分帧融合在Lyon算法中,帧长与No.1对齐,帧移3.2ms | 64 | (104, 64) | 98.6667 |
| 4 | No.2 + 不加窗 | 64 | (43, 64) | 97.8333 |
| 5 | No.3 + 不加窗 | 64 | (104, 64) | 98.3333 |
| 6 | 将分帧融合在Lyon算法中,帧长200,帧移80 | 200 | (33, 64) | 97.8333 |
| 7 | 先分帧(帧长64,帧移25.6),再对每一帧使用原始Lyon算法 | 64 | (104, 64) | 13.0000 |
| 8 | 先分帧(帧长200,帧移80),再对每一帧使用原始Lyon算法 | 200 | (33, 39) | 10.5000 |
| 9 | MFCC,帧长64,帧移25.6 | 64 | (104, 39) | 6.8333 |
| 10 | MFCC,帧长200,帧移80 | 200 | (33, 39) | 11.6667 |
| 11 | No.3 + 中心化 | 64 | (104, 64) | 12.0000 |
| 12 | No.10 + 中心化 | 200 | (33, 39) | 99.0000 |
- 有一定的帧重叠并且加窗是能提高识别率的
- 帧长200,帧移80,对应的是,帧长25ms,帧移10ms,与MFCC中的默认配置一致
- Lyon不宜处理过长的帧
- MFCC加上中心化后才能发挥出效果,否则性能远低于Lyon【具体原因?】
- 为什么Lyon中心化后识别效果反而不好了?
- Whatever,可以得出结论,MFCC又快又好!
我们基于TIMIT数据集,用DNN/RNN做实验对比两个特征:
| Model | 特征 | Dim | Acc[%] |
|---|---|---|---|
| RNN | MFCC | 41 | 56.3654 |
| Lyon | 86 | 33.8048 | |
| DNN | MFCC | 164 | 48.5015 |
| Lyon | 344 | 33.7413 |
*上述特征处理均采用原始算法,没有进行帧对齐
综合两个实验,我们基本可以得出结论:MFCC比Lyon运算速度快,且识别效果好。
# 参考资料
- 数据预处理:数据的正态化和标准变换_一道微光的博客-CSDN博客_数据正态化处理 (opens new window)
- 标准化和归一化的区别、应用场景? - 知乎 (zhihu.com) (opens new window)
# Ikeda-based system
$$\dot{x}(t)=-x(t)+\mu f\left(x\left(t-t_{\mathrm{R}}\right)\right)$$
其中,$f(x)=\sin \left(x-x_0\right) \quad\left(x_0=\text { const }\right)$
- 一种非线性光学腔行为的数学模型,被用于理解各种非线性光学系统的行为,并被用作开发和评估求解非线性微分方程的新数值方法的测试案例
DRC之前使用的是Mackey-Glass动力系统,现在推导Ikeda下的求解器,应该用怎样的Ikeda表达式呢?使用DRC提出者的学位论文中的化简表达式:
$$\dot{x}(t)=-x(t)+\eta \sin ^2[x(t-\tau)+\zeta J(t)+\phi]$$
根据学位论文中的数值仿真结果,最佳实验参数配置为$\eta=0.3$,$\zeta=0.5$,$\phi=0.9\pi$。不同任务下的最佳参数配置需要通过网格搜索确定。类似于MG系统,用隐式中点法得到迭代式:
$$\left( 1+\frac{h}{2} \right) X\left( t_n+h \right) =\left( 1-\frac{h}{2} \right) X\left( t_n \right) +h\times \eta \sin \left[ X\left( t_n+\frac{h}{2}-\tau \right) +\zeta J\left( t_n+\frac{h}{2} \right) +\phi \right]$$
其中,$\phi$用于调节非线性,类似于MG系统中的指数$p$。
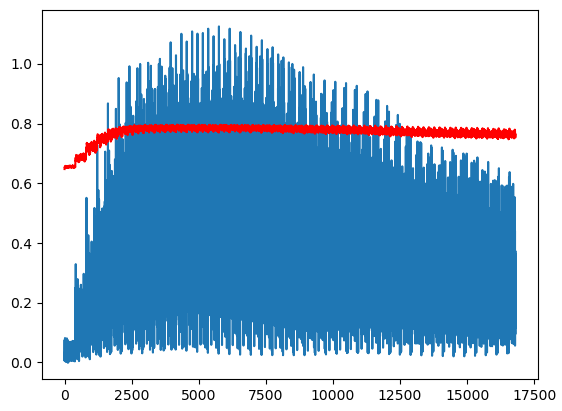
# 输入与响应
- 使用的是Lyon特征
| Mackey-Glass | Ikeda |
|---|---|
 |  |
# 稳态响应与瞬态响应
- Ikeda使用的是学位论文中的配置
- 仅调节了$\tau$
| $\tau=80$ | $\tau=800$ | $\tau=8000$ | |
|---|---|---|---|
| MG | 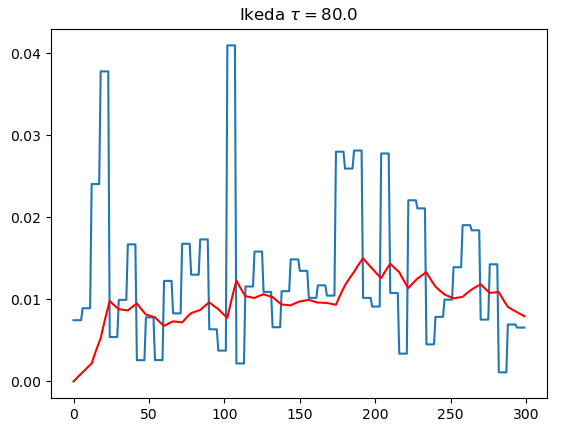 | 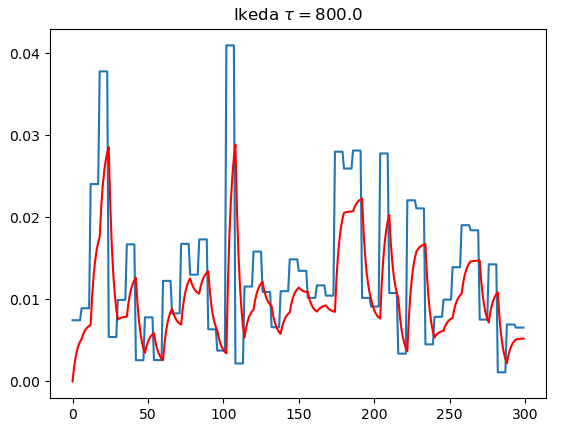 | 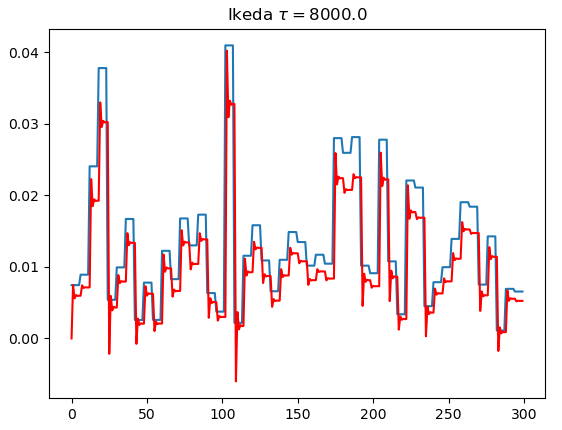 |
| Acc | |||
| Ikeda | 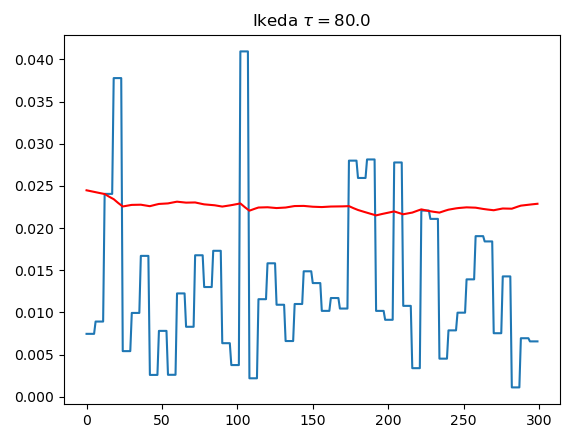 | 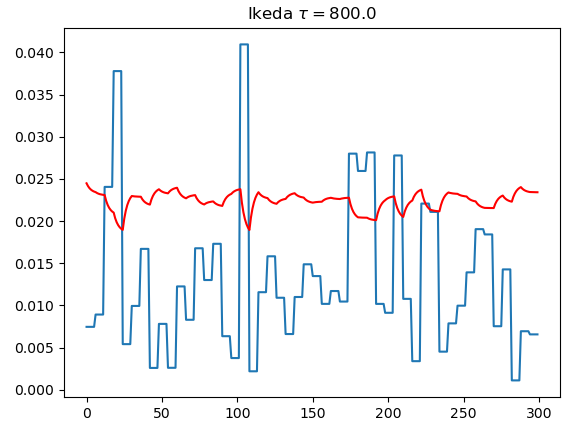 | 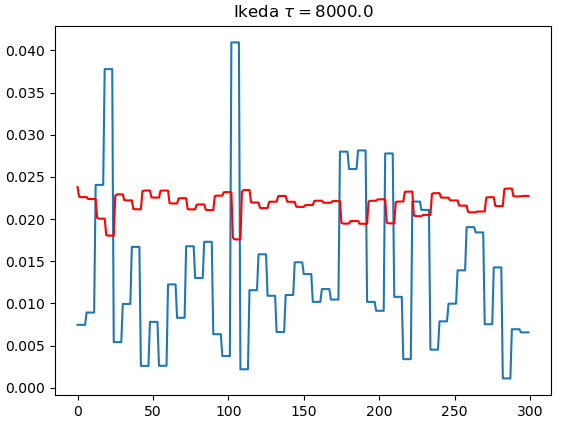 |
| Acc |
# 时间参数的影响
- Ikeda与MG系统做了统一,输入增益均为0.5,反馈增益均为0.8,MG的指数$p=7$,Ikeda的相位$\phi=0.15\pi$
- Ikeda的迭代式用的是常数变易公式,MG用的是隐式中点法;
| System | N | $\theta$ | $\tau$ | N_step(=6N) | Acc[%] |
|---|---|---|---|---|---|
| Ikeda | 400 | 0.2 | 80 | 2400 | 83.1667 |
| 50 | 1.6 | 80 | 300 | 83.1667 | |
| 40 | 2 | 80 | 240 | 78.8333 | |
| 50 | 2 | 100 | 300 | 83.1667 | |
| MG | 400 | 0.2 | 80 | 2400 | 85.5 |
| 50 | 1.6 | 80 | 300 | 85.5 | |
| 40 | 2 | 80 | 240 | 80.5 | |
| 50 | 2 | 100 | 300 | 85.3333 |
*执行脚本:mainDRC.py
- 仿真结果表明,MG效果比Ikeda好
- 系统的瞬态响应是DRC成功运行的关键
- 只要不是彻底达到稳态响应,识别效果并不会下降,即$\theta>>1$才不行
# 参考资料
- Midpoint method - Wikipedia (opens new window)
- 如何理解「混沌理论」,它有什么特性,有哪些著名的例子? - 知乎 (zhihu.com) (opens new window)
- pe-ge/Computational-analysis-of-memory-capacity-in-echo-state-networks (github.com) (opens new window)
- 使用Python绘制一个非常漂亮的李雅普诺夫指数,及其函数值_lyapunov函数python_fK0pS的博客-CSDN博客 (opens new window)
- 求最大李雅普诺夫指数(Largest Lyapunov Exponents,LLE)的 Rosenstein 算法_颹蕭蕭的博客-CSDN博客_最大李指数 (opens new window)
- Lyapunov指数--大连民族大学
- “Computational analysis of memory capacity in echo state networks”
- “Backpropagation algorithms and Reservoir Computing in Recurrent Neural Networks for the forecasting of complex spatiotemporal dynamics”
# 硬件实现
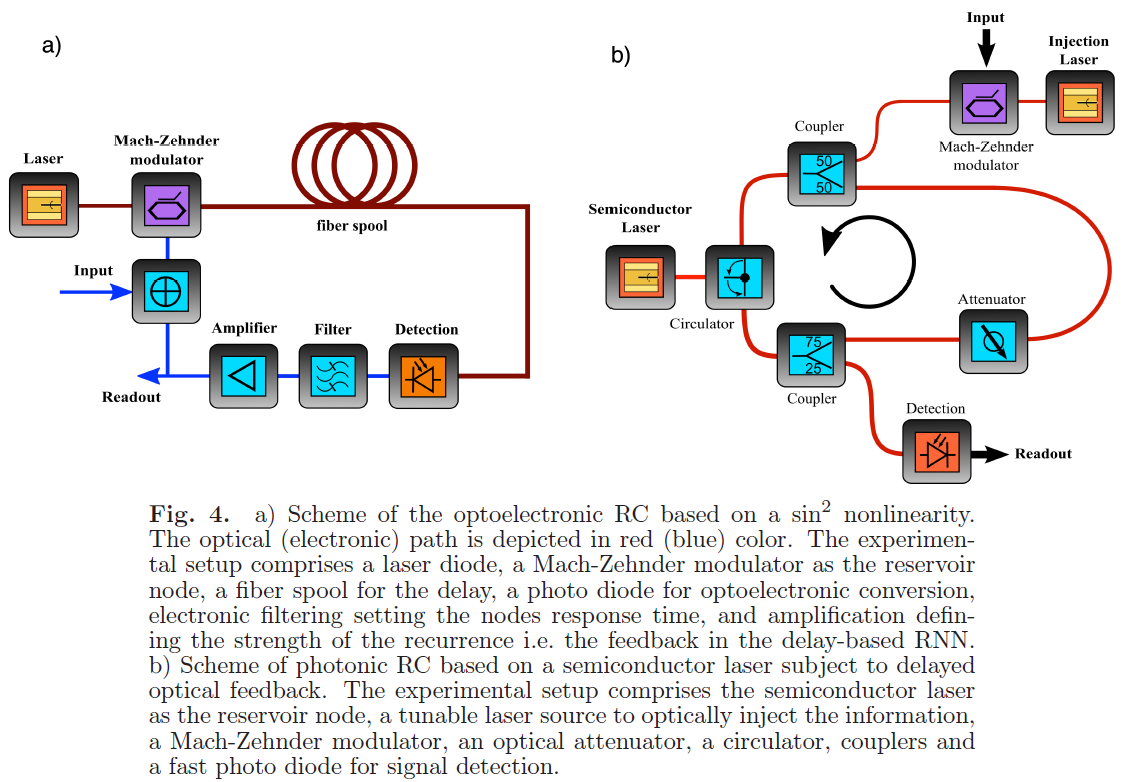
(a) 光电实现:实验装置包括一个激光二极管、一个作为储存器节点的Mach-Zehnder调制器、一个用于延迟的光纤线轴、一个用于光电转换的光电二极管、设置节点响应时间的电子滤波以及定义递归强度的放大器,即基于延迟的RNN中的反馈部分。
(b) 全光学实现:
参考文献:Nonlinear photonic dynamical systems for unconventional computing
# 相关项目
🚩Dynamic Networks with Time Delays and Adaptation: Theory and Applications (411803875)
耦合动态系统的网络可作为各种应用的模型。在现实系统的建模中,由于组件之间的有限信号传播,自然会出现时间延迟。此外,如果网络是自适应的,即其拓扑结构随时间变化,则生成的系统将成为理论研究的复杂对象。到目前为止,时间延迟和适应性的影响通常是单独或用纯数值方法研究的。**该项目的目的是研究时间延迟和自适应网络结构对现实动态网络模型动力学的影响。**该项目的主题包括以下问题:
- 延迟系统中的普遍性类,临时耗散孤子;
- 自适应网络中复杂模式的稳定性;
- 具有不同时间尺度和不同适应规则和/或多个延迟的耦合系统的同步;
- 非线性主动光学网络的动力学研究;
与外部合作伙伴合作,该项目旨在探索使用具有时间延迟的自适应动态系统的机器学习应用的新概念。除了耦合光电系统之外,还将考虑电网,特别是它们与自适应神经网络的关系。
🚩Dynamic Phenomena in Complex Networks: Basics and Applications(RTG 1740)
迄今为止,大多数研究的重点都是固定不变的拓扑结构;因此,分析的范围受到严重限制。在我们的iGRK中,我们研究了时变复杂网络中的自组织原理。为了使这些方法更加现实,还将研究网络异质性、多尺度、时间延迟和随机源的影响。这些理论研究与日益复杂的实验和自然网络的研究密切相关,从电网到感染网络,从神经元网络到地球系统。后者是我们将特别关注的一个挑战。因此,研究培训小组的一个主要主题也将是了解地球在不断变化的条件下的子系统。特别是,对全球变暖和亚马逊地区土地利用变化等影响进行了调查。
# 一些Chat GPT的回答
外耳、中耳和内耳对语音信号不同频率的响应?
外耳、中耳和内耳对不同频率语音信号的反应对我们感知和理解语音至关重要。 外耳充当一个漏斗,收集声波并将其导入耳道。由于其在高频处的共振,它具有高频率响应,并且这种共振也有助于提高耳朵在较高频率下的灵敏度。 中耳在小骨(中耳骨)的帮助下放大和过滤声波。它具有有限的频率范围,可以有效放大,最高灵敏度约为2-4 kHz。这种放大有助于克服发生在外耳和内耳的能量损失,使内耳更容易检测声音信号。 内耳将机械振动转化为可由大脑处理的电信号。它在4-8kHz左右的频率上具有高灵敏度,对低频不太敏感。这个范围对于语音识别很重要,因为语音信号包含这些频率范围内的大部分能量。内耳也有一个称为耳蜗滤波器的专门滤波系统,它可以提高语音信号中不同频率分量的分辨率。 总的来说,外耳、中耳和内耳对不同频率的语音信号的不同反应共同提高了我们感知和理解语音的能力。
滤波器中的中心频率和质量因子是什么?
中心频率是指滤波器的频率响应的最大值,代表了滤波器最敏感的频率。质量因子是指滤波器的频率响应的带宽,代表了滤波器的频率敏感程度。一般来说,频带抑制就是通过控制中心频率和质量因子来抑制不需要的信号频率。
陷波滤波器、谐振器、零点与极点之间的关系?
滤波器中陷波、谐振器、零点和极点之间的关系可以描述如下:
陷波:陷波是滤波器显著抑制或“陷波”的频带。陷波滤波器被设计为抑制特定频率或频带。 谐振器:谐振器是一种滤波器,设计用于谐振或放大特定频率的信号。它通过以特定频率谐振并拒绝该频带之外的信号来工作。 零:零是滤波器的传递函数值为零的频率。换句话说,该频率的信号被滤波器完全抑制。零用于实现滤波器中的陷波。 极点:极点是滤波器传递函数接近无穷大的频率。具有极点的滤波器能够放大这些频率的信号。极点的位置决定了滤波器的频率响应。 总之,陷波器、谐振器、零点和极点都是用于设计滤波器的部件。陷波和零点用于抑制特定频率下的信号,而谐振器和极点用于放大特定频率下信号。
为什么谐振器峰值应该在陷波滤波器的下边缘?
谐振器峰值应位于陷波滤波器的下边缘,以产生能有效地减少特定频率范围的能量的带阻或陷波滤波器,同时允许其他频率范围以最小的减少通过。谐振器在陷波频率的下边缘产生传递函数的峰值,这补偿了陷波滤波器引起的能量损失。这导致具有最小失真的平坦通带,使其成为实现频率选择性滤波的有效方式。
什么叫谐振器峰值应该在陷波滤波器的下边缘?
谐振器峰值位于陷波滤波器的下边缘意味着谐振器被设计为提高陷波的下边缘处的频率,或被陷波滤波器抑制的频率。这样做是为了补偿陷波滤波器引起的这些频率中的能量损失,并恢复频率响应的总体平衡。将谐振器峰值放置在陷波滤波器的下边缘的原因是确保谐振器不会干扰陷波滤波器预期的目的,即抑制不希望的频率。通过将谐振器峰值放置在陷波滤波器的下边缘,谐振器能够恢复抑制频率中的能量,而不影响陷波滤波器想要抑制的频率。
陷波滤波器的下边缘是指陷波的频率下限或滤波器开始抑制的频率。陷波滤波器用于抑制或抑制信号中的特定频率或频率范围,陷波滤波器的下边缘指示该频率范围的下限。谐振器峰值应放置在陷波滤波器的下边缘,以确保对不期望的频率或频率范围的最大抑制。
为什么滤波器的最高频率还取决于零点位置?
滤波器中零点的位置决定滤波器的幅度响应。滤波器的幅度响应描述了输入信号的幅度受滤波器影响的程度。滤波器的最高频率取决于零点的位置,因为零点决定了滤波器的幅度响应达到其最大值的频率,即通带。零点的位置决定了滤波器在通带区域的幅度响应的斜率,这会影响滤波器的最高频率。如果零点相距太远,幅度响应将具有陡峭的斜率,这将导致窄通带和低顶部频率。如果零点太靠近,幅度响应将具有平坦的斜率,这将导致宽通带和高顶部频率。因此,滤波器的最高频率取决于零点的位置,并且可以通过调整零点的位置来调整。
滤波器中的AGC作用?
滤波器中的AGC指的是自动增益控制,这是一种自动调整放大器增益以保持恒定输出电平的电路。在滤波器的情况下,AGC通常用于调节输入信号电平,确保信号保持在特定范围内,即使输入电平改变。这有助于防止信号链中后续级的过载,以及确保输出信号保持在一致的电平,而不管输入信号的波动。AGC通常用于诸如无线电接收机、放大器和输入信号电平可以广泛变化的其他系统的应用中。
$V_{out} = K * V_{in} * (V_{ref} / V_{in})^α$,$α$的值经常被调整以平衡AGC环路速度和输出信号中噪声水平之间的折衷。高$α$值将导致快速AGC响应,但也可能导致输出信号中的噪声增加。较低的$α$值将导致较慢的AGC响应,但通常会产生较干净的输出信号和较少的噪声。值得注意的是,该方程是AGC电路的简化表示,实际的AGC电路可能更复杂,包括各种反馈机制、补偿元件和其他组件。
