 专业英语_中文综述大纲
专业英语_中文综述大纲
# 基本要求
题目:非冯诺依曼结构下的神经网络构建/神经形态计算/物理神经网络/Photonic Neural Network
时长:20min
汇报日期:2022.10.17
# 研究背景
# 深度学习基本流程(P1)
数据预处理——信号前向传播——误差反向传播——参数更新
参考文献:
# 传统网络结构(P2)
DNN
RNN(时序信号处理:语音、文本)
CNN(图像处理)
GAN(生成对抗网络)
其核心思想来自于博弈论的"纳什均衡“。它包含两个网络模型:一个生成模型和一个判别模型。生成模型捕捉样本数据的分布,判别模型是一个二分类的分类器。生成模型接受一个随机的噪声,结合学习到的样本数据特征,生成一个新的数据,交由分类模型去判断是否是“真实的”,在训练过程中,生成模型尽量生成新数据去欺骗判断模型,判断模型会尽量去识别出不真实的数据,两者实际上是一个“二元极小极大博弈问题”。最终得到一个生成模型可以从来生成新的数据。
参考资料:
- 神经网络算法详解 05:其他神经网络简介(DNN、CNN、RNN、DBN、GAN等)_datamonday的博客-CSDN博客_神经网络算法种类 (opens new window)
- Main Types of Neural Networks and its Applications — Tutorial | Towards AI (opens new window)
- The mostly complete chart of Neural Networks, explained | by Andrew Tch | Towards Data Science (opens new window)
# 冯诺依曼瓶颈(P3)
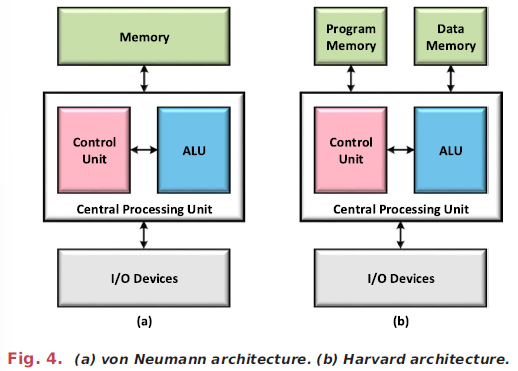
超级计算机在物理上分离了核心内存和处理单元,这会减缓他们的速度,并大幅增加他们的能源消耗。这种“冯·诺依曼瓶颈”是人工智能算法的一个问题,它要求在每一步读取大量数据,对这些数据执行复杂操作,然后将结果写回内存24。这种数据传输过程减慢了计算速度,大大增加了学习和推理的能耗。
然而,它们运行的硬件,如图形处理单元或张量处理单元,限制了它们在大型、特别是能源密集型数据中心之外的开发。因此,开发更适合运行当前神经网络的硬件是一个重要的挑战。
# 非冯诺依曼计算平台(P4)
耗能:通俗比方,蠕虫和计算机
第一种方法是将目前在人工智能中使用的传统神经网络算法映射到专用物理系统,以提高其实现的能效。第二种方法是超越这些算法,从神经科学中获得灵感,为人工神经网络配备额外的功能和动力学,希望实现更复杂的计算。
【插入常见非冯诺依曼计算平台的应用】
说明:侧重网络设计,后面以光学为例
# 网络复刻(P5)
| CMOS+忆阻器 | 全光学系统/光电混合系统 |
|---|---|
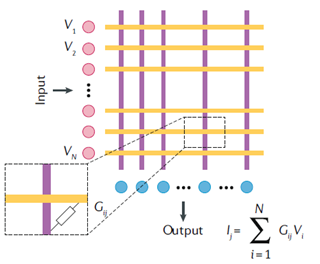 | 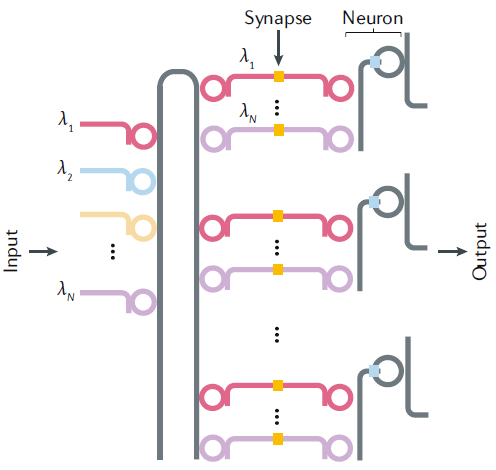 |
| 在混合CMOS/记忆系统中,神经元由模拟或数字CMOS组成,流经网络的信息是电流。因此,为了调节信息流,突触应该充当电流的阀门。这种阀门可以用记忆电阻器实现(“记忆电阻”的缩写,也称为电阻开关器件)。 |
问题:
- 在传统计算机上训练好后移植过来,精度不够?
- 元器件太多,需要精密调谐
# 类脑:Spiking Neural Network(P10)

主要讲
为什么脉冲神经网络在非冯诺依曼结构上有广泛应用?
# 折叠:延迟动力系统
# Reservoir Computing:环状拓扑
基本原理(P6)
Reservoir Computing Time-delayed Reservoir Computing 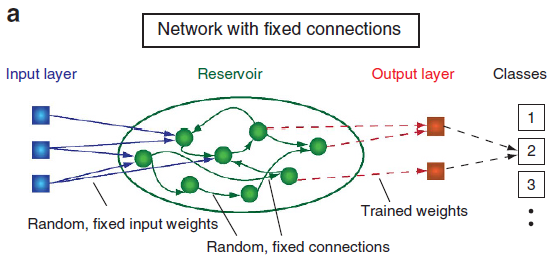
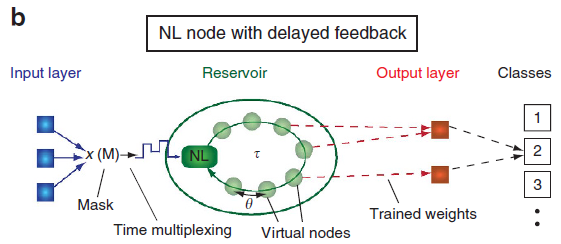
参考文献:《Information processing using a single dynamical node as complex system》
网络变种:Deep Time-delayed Reservoir Computing
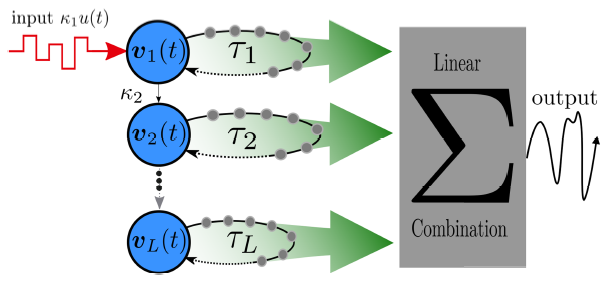
参考文献:《Deep time-delay reservoir computing: Dynamics and memory capacity》
应用与分析(P7)
# 任意拓扑(P8)
参考文献:《Experiments with arbitrary networks in time-multiplexed delay systems》
问题:隐藏层不可训练,反向传播是大规模网络训练的必要手段
# Folded-in-time DNN(P9)
基本原理
折叠形态 展开形态 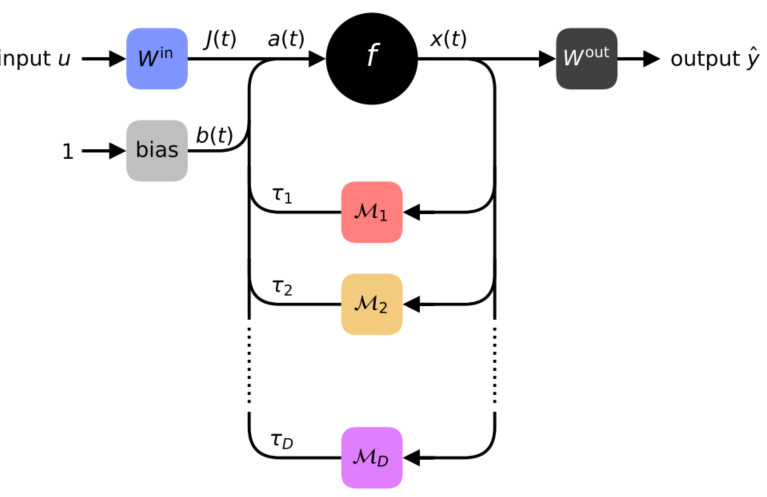
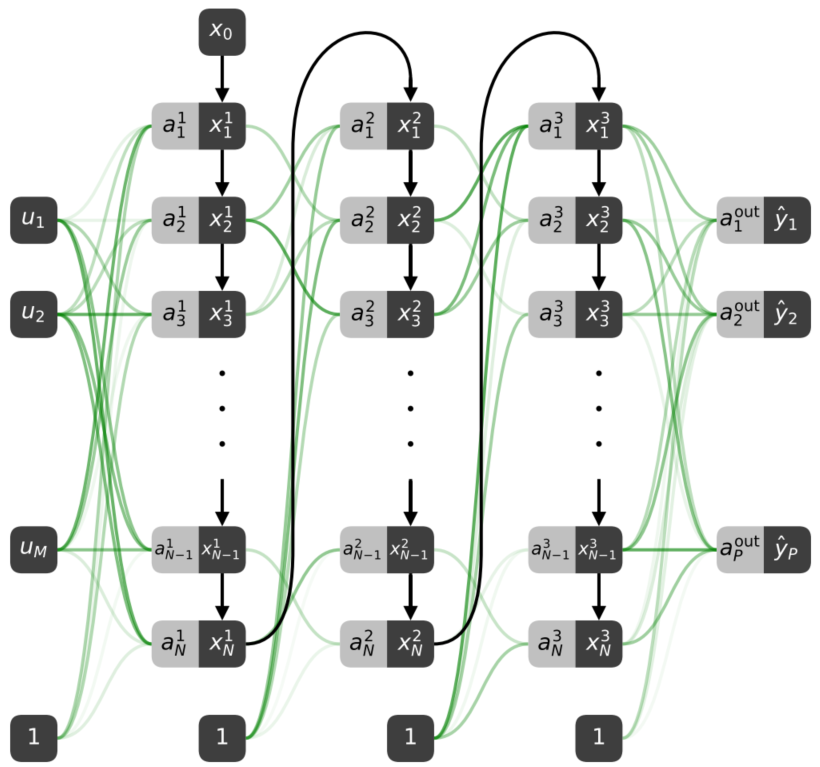
参考文献:《Deep neural networks using a single neuron: folded-in-time architecture using feedback-modulated delay loops》
过渡:因为前向传播是物理过程,无法在原位进行反向传播
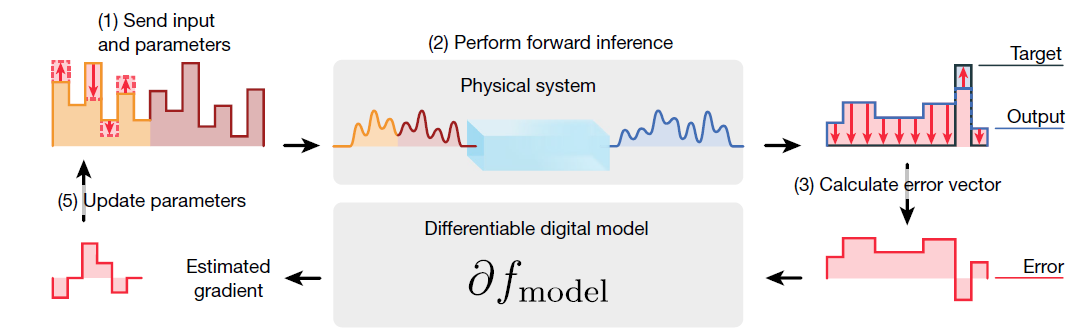
# 支持原位训练:Physics-awared Training(P11)
将反向传播应用于训练可控物理系统。正如深度学习使用由数学函数层构成的深度神经网络实现计算一样,我们的方法允许我们训练由可控物理系统层构成的深层物理神经网络,即使物理层与传统人工神经网络层缺乏任何数学同构。 为了证明我们方法的普遍性,我们训练了基于光学、力学和电子学的各种物理神经网络,以实验方式执行音频和图像分类任务。物理感知训练结合了反向传播的可伸缩性和原位算法可实现的缺陷和噪声的自动缓解。物理神经网络有潜力比传统电子处理器更快、更节能地执行机器学习,更广泛地说,它可以赋予物理系统自动设计的物理功能,例如机器人23–26、材料27–29和智能传感器30–32。
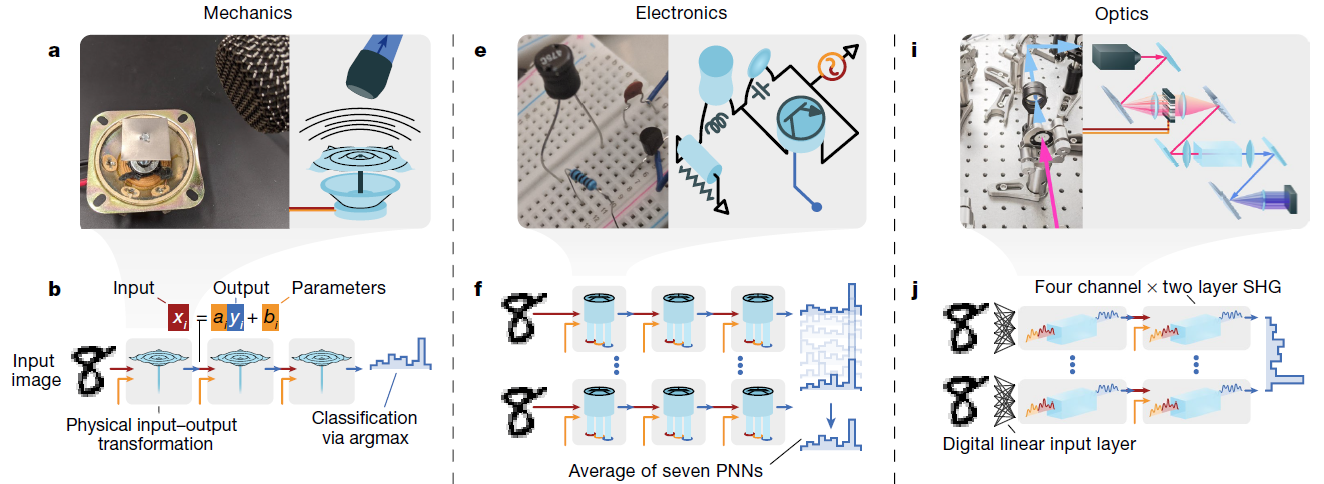
如何训练?
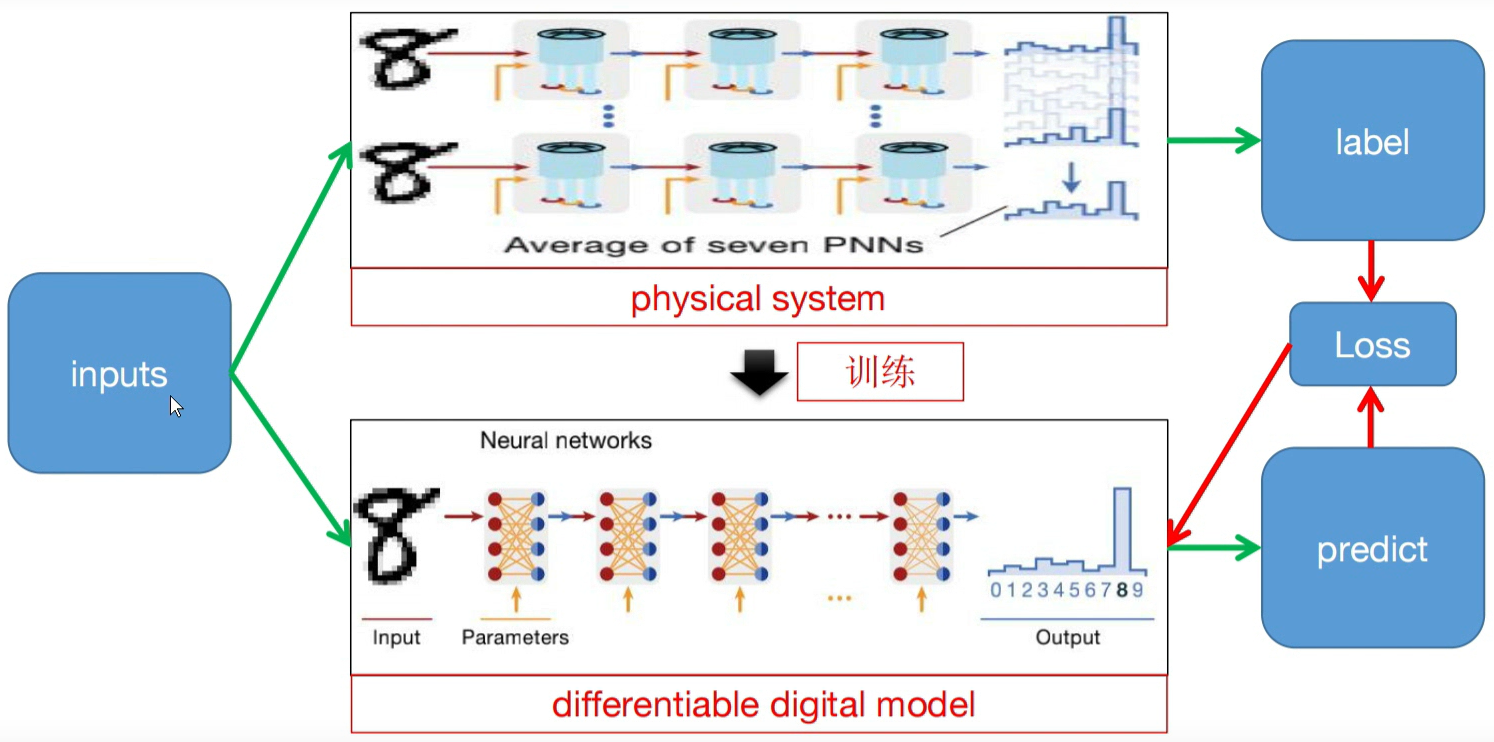
| 验证模型训练的有效性 | 验证PAT训练方法的有效性 |
|---|---|
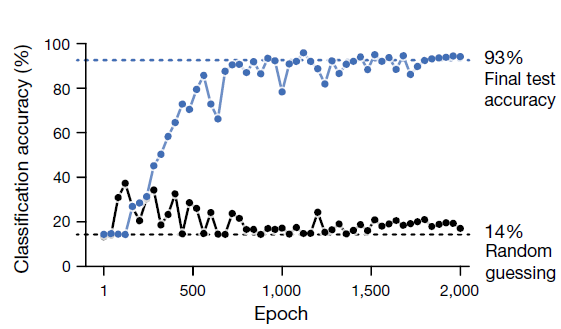 | 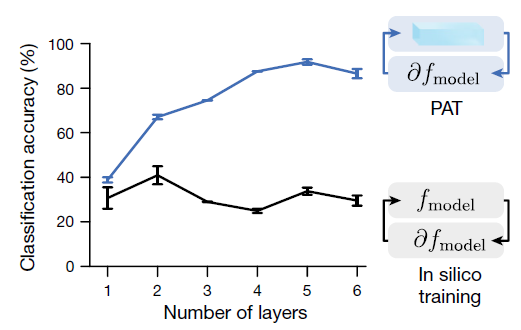 |
参考文献:
- 《Deep physical neural networks trained with backpropagation》
- nature-文献阅读-深度学习新方法PNN(反向传播训练的深层物理神经网络)_哔哩哔哩_bilibili (opens new window)
# 前景与挑战(P12)
算法层面
- 前后向传播不一致:前向物理过程不能解析微分,只能近似估计,用数值模拟训练物理系统,造成模拟-现实差距【层数越深越明显】
大规模硬件部署
精度问题:大多数纳米器件本身就有噪声,其有效重量值不会完全连续变化
首先,在神经形态计算中,纳米突触和纳米神经元之间的紧密高效互连是一个很大的困难。
非线性运算:物理元器件的非线性函数不是那么理想化的
迁移导致精度降低
# 疑问
- 如果SNN是非冯诺依曼结构的基本算法,那么RC之类的算什么
# 参考文献
- 《Physics for neuromorphic computing》
