背景

• TRC将延迟动力系统与机器学习做结合，但网络结构具有局限性
• 非冯诺依曼下的硬件搭建费用高昂且困难

原理

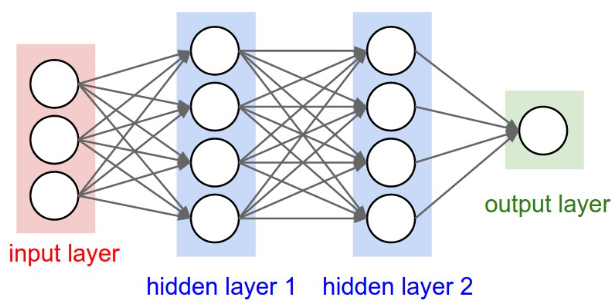
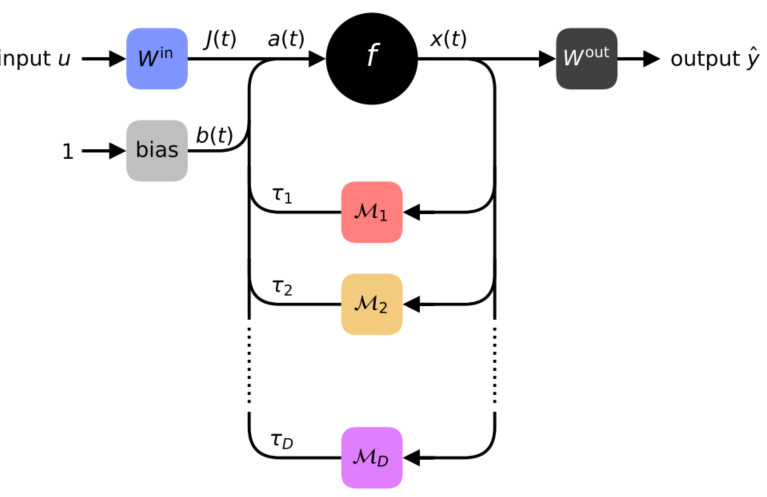
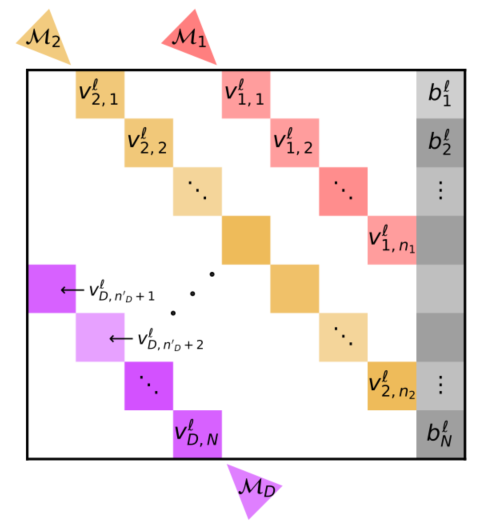
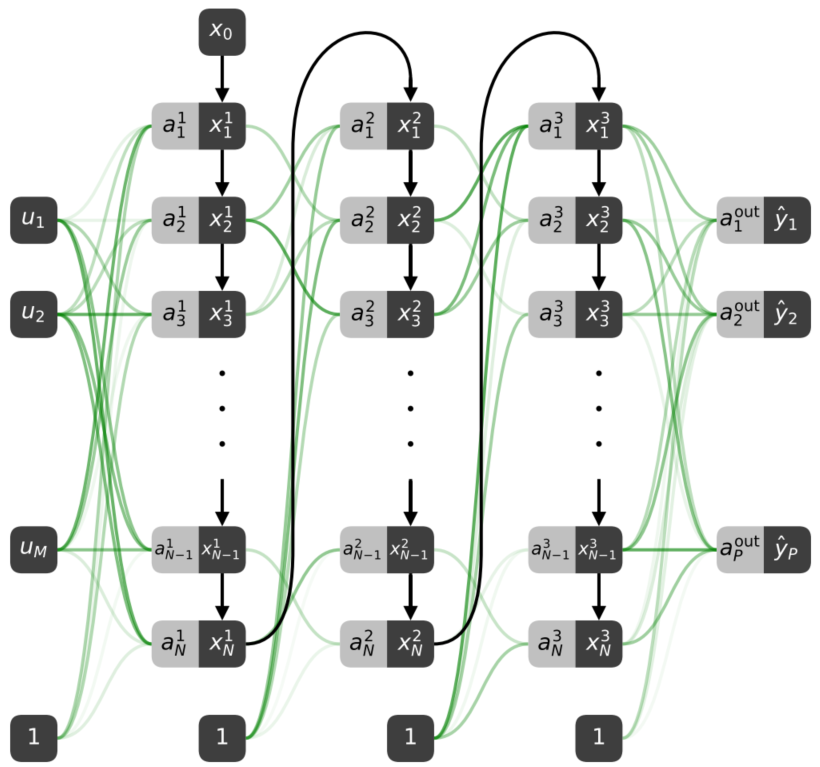
将空间需求转为时间需求，用延迟系统依次模拟网络中的每一个节点，上一层节点信号通过延迟环传输，最终将网络折叠为一个非线性神经元和几个带有反馈调制模块的延迟环：

时滞微分方程(DDE)：$\dot{x}(t)=-\alpha x(t)+f(a(t))$，其中$a(t)=J(t)+b(t)+\sum_{d=1}^{D} \mathcal{M}{d}(t) x\left(t-\tau{d}\right)$，通过对微小区间进行积分，可以得到迭代更新公式，从而计算解析解。

特点：

• 延时模块个数（即延迟环数量）只取决于单层神经元的个数，与网络层数无关
• 当节点间距$\theta$较大时，性能与传统DNN一致；$\theta$较小时，计算速度会变快，但精度会略有下降
• 实验表明，并不需要全连接，用稀疏权重矩阵就能获得很好的性能（动态稀疏矩阵在传统神经网络中已经证明了先进性，但是本文是固定的稀疏矩阵）
• 与DNN相比，$\theta$较小时，相邻节点之间有耦合影响
• 前向传播可以是in situ，反向传播必须是in silico

缺点：

• 不可以并行计算，训练时间很长，但是推断的时候，计算量小，且模型大小相当小
• 目前只实现了固定节点数的全连接层，作者指出CNN的实现可以考虑分布式延迟（声纹识别需要CNN网络）

求解器推导

延迟系统模型：

$$\mathrm{x}{\mathrm{n}}^1=\mathrm{e}^{-\alpha\theta}\mathrm{x}{\mathrm{n}-1}+\int_{\mathrm{t}_0}^{\mathrm{t}_0+\theta} \mathrm{e}^{\alpha\left(\mathrm{s}-\left(\mathrm{t}_0+\theta\right)\right)} \mathrm{f}(\mathrm{a}(\mathrm{s})) \mathrm{ds}$$

• solver_coupled

$$ \mathrm{x}{\mathrm{n}, \mathrm{n}{\mathrm{h}}}=\mathrm{e}^{-\alpha \times \mathrm{n}{\mathrm{h}} \times \mathrm{h}} \mathrm{x}{\mathrm{n}-1, \mathrm{~N}{\mathrm{h}}}+\alpha^{-1}\left(1-\mathrm{e}^{-\alpha \times \mathrm{n}{\mathrm{h}} \times \mathrm{h}}\right) \mathrm{f}\left(\mathrm{a}_{\mathrm{n}}^1\right) $$

• solver_dde_ibp

$x_{n,n_h}=e^{-\alpha h}x_{n,n_h-1}+\int_{t_0+\left( n_h-1 \right) \times h}^{t_0+n_h\times h}{e^{\alpha \left( s-\left( t_0+n_h \right) \right)}f\left( a\left( s \right) \right) \mathrm{d}s}$

$=e^{-\alpha h}x_{n,n_h-1}+\alpha ^{-1}e^{\alpha \left( s-\left( t_0+n_h \right) \right)}f\left( a\left( s \right) \right) \mid_{t_0+\left( n_h-1 \right) \times h}^{t_0+n_h\times h}+\int_{t_0+\left( n_h-1 \right) \times h}^{t_0+n_h\times h}{\alpha ^{-1}e^{\alpha \left( s-\left( t_0+n_h \right) \right)}\dot{f}\left( a\left( s \right) \right)}\mathrm{d}s$

$\approx e^{-\alpha h}x_{n,n_h-1}+\alpha ^{-1}e^{\alpha \left( s-\left( t_0+n_h \right) \right)}f\left( a\left( s \right) \right) \mid_{t_0+\left( n_h-1 \right) \times h}^{t_0+n_h\times h}+\int_{t_0+\left( n_h-1 \right) \times h}^{t_0+n_h\times h}{\alpha ^{-1}e^{\alpha \left( s-\left( t_0+n_h \right) \right)}\mathrm{d}s}*\frac{f\left( a\left( t_0+n_h\times h \right) \right) -f\left( a\left( t_0+\left( n_h-1 \right) \times h \right) \right)}{h}$

$=e^{-\alpha h}x_{n,n_h-1}+\alpha ^{-1}\left( f\left( a_{n,n_h} \right) -f\left( a_{n,n_h-1} \right) e^{-\alpha h} \right) +\frac{1-e^{-\alpha h}}{\alpha ^2h}\left( f\left( a_{n,n_h} \right) -f\left( a_{n,n_h-1} \right) \right)$

• 用更精确的积分模型计算有何意义呢？更贴近实际情况

• 深度学习延时系统solve_dde_ibp_qq_41093957的博客-CSDN博客 (opens new window)

Fit-DNN VS DRC

基于TIMIT数据集，考察两个折叠网络的性能

动态组合延迟环

Fit-DNN在有限的延迟环数量及长度下，为了最大限度使用延迟环，使得隐藏层之间的权重矩阵的稀疏形式固定，且隐藏层的节点数均相同，限制了网络形式。

Fit-DNN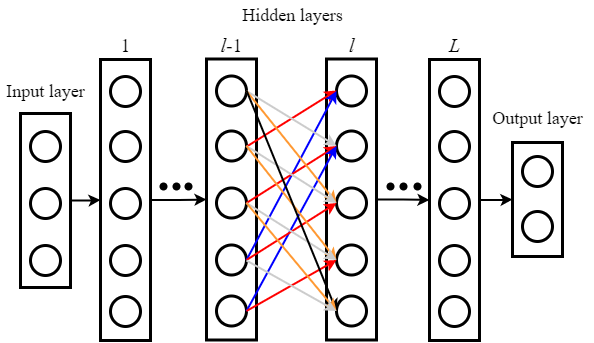
等宽DNN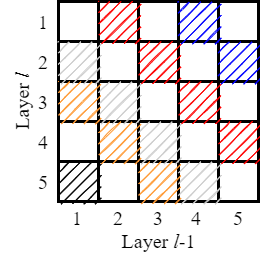
动态连接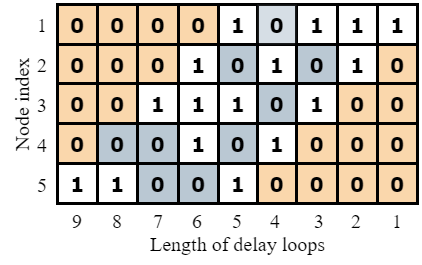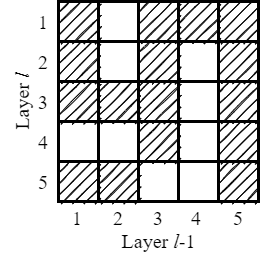
自动编码器		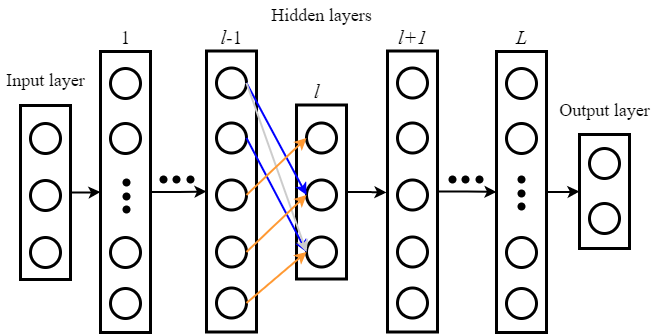此时延迟环最大数量为$\max(N_{l-1}+N_l-1)$
动态连接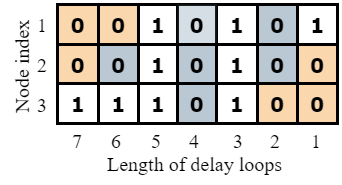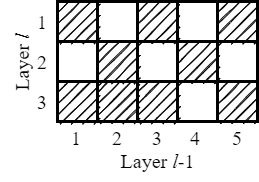

原文中，由于只与前一层连接的限制，使得部分节点并不是接收所有延迟环反馈回来的信号。因此，对于其他满足条件的节点，我们也可以动态选择需要的延迟环信号，可以消除三种限制：

• 消除删除一条延迟环就删除全部对角元素的限制
• 消除隐藏层间稀疏矩阵形式一致的限制
• 消除每个隐藏层节点数相同的限制

实验结果

• 等宽DNN

  • 当稀疏度一致时，延迟环动态连接的识别准确率较高，但是系统所需的延迟环数达到最大，即(2N-1)

  • 当隐藏层节点数为50，最大延迟环数为99，随机选取40个长度的延迟环时，动态连接的识别率略有下降；但是延迟环数与动态连接的关系还需要进一步探索

• 变宽DNN/自动编码器

  • 在当前10人的小规模识别中，变宽DNN并不比等宽DNN具有优势

  • 至少是三层隐藏层结构，完成了[80,50,80]，[50,30,50]两种结构，后者准确率更高，但是这个是根据识别规模需要做出调整的

  • 完成了[80,50,80]下全连接状态和稀疏度为0.1下的对比，稀疏矩阵具有优势