 Fit-RNN原理及应用
Fit-RNN原理及应用
主要工作节点:
- [x] Fit-RNN的实现:前后向传播的修改
- [x] 与Fit-DNN的对比:为什么不直接在输入端考虑前后帧?
- [x] 修改非线性函数后对比:sin>tanh
- [x] 与Reservoir Computing的比较
- [x] Lyon VS MFCC:MFCC
- [x] 基于Ikeda的DRC
- [x] 三个模型的对比:长语音、短语音
# RNN相关
# RNN原理
| DNN | RNN |
|---|---|
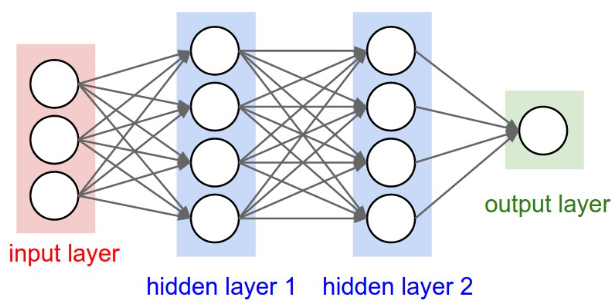 | 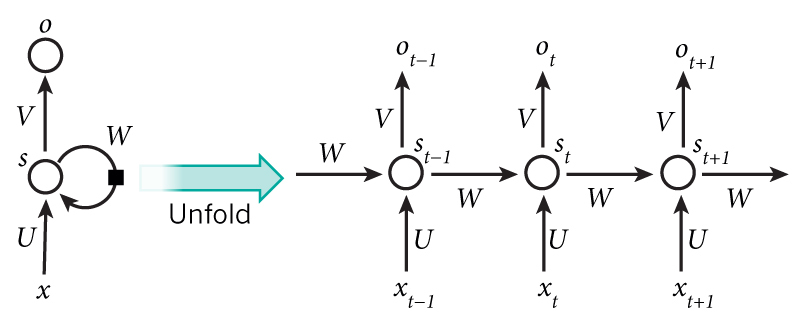 |
| $\boldsymbol{a}^l=\sigma\left(\boldsymbol{W}^l \boldsymbol{a}^{l-1}+\boldsymbol{b}^l\right)$ | $\boldsymbol{h}^{(t)}=\sigma\left(\boldsymbol{U} \boldsymbol{x}^{(t)}+\boldsymbol{W} \boldsymbol{h}^{(t-1)}+\boldsymbol{b}\right)$ |
| Fit-DNN | Fit-RNN |
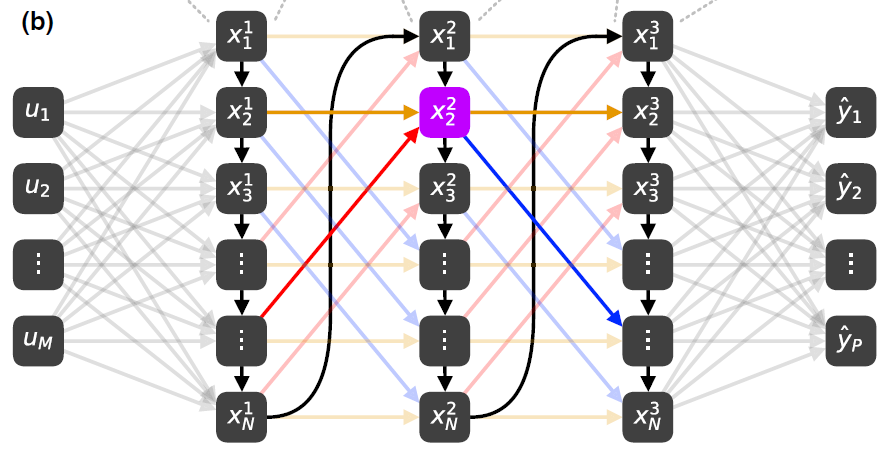 | 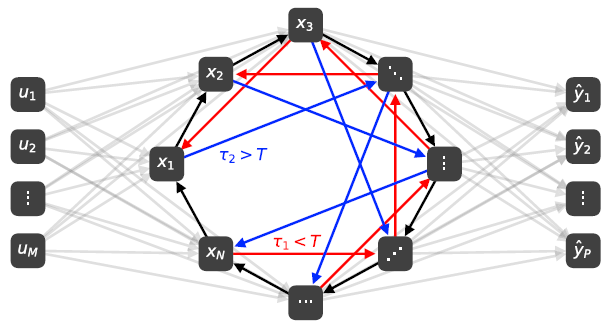 |
- RNN更适合时序信号的处理,例如文本、语音、天气预测等
- 对于单层RNN,每个时间步都需要输入input data,只是每个时间步的input data不同罢了
- DNN中每个隐藏权重矩阵不同,而RNN每个时间步共享隐藏权重矩阵
- 以单层RNN为例,非线性激活函数同时作用于输入层至隐藏层和不同时间步之间;而DNN中,非线性激活函数分别作用于输入层至隐藏层和相邻隐藏层之间,且函数形式不必一致
- ==DNN是最后一个隐藏层连接输出层,RNN是所有时间步的输出求均值后连接输出层==
❗问题:
- RC中的虚拟节点也是有本地连接的吗?是的
# RNN反向传播[BPTT]
沿着时间轴累加
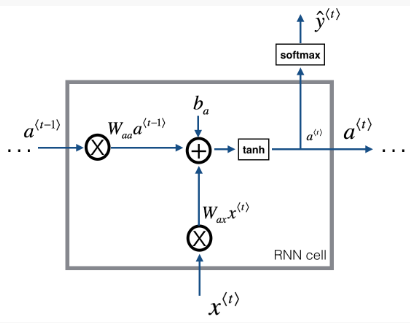
隐藏层状态:
$$a_t=\tanh \left(W_{a, x} * X+W_{a, a} * a_{t-1}+b_a\right)$$
输出值:
$$y_{\text {pred }}=\operatorname{softmax}\left(W_{y, a} * a_t+b_y\right)$$
注:本文不是每一步都生成预测值,而是对隐藏层状态取均值
损失函数求导:
$$\frac{\partial J}{\partial y}=Y_{\text {pred }}-Y$$
输出值的权重和偏置的求导:
$$\frac{\partial J}{\partial W_{y, a}}=\frac{\partial y}{\partial W_{y, a}} * \frac{\partial J}{\partial y}=a * \frac{\partial J}{\partial y}$$
$$\frac{\partial J}{\partial b_y}=\frac{\partial J}{\partial y}$$
隐藏层状态的求导:
$$\frac{\partial J}{\partial a}=\frac{\partial y}{\partial a} * \frac{\partial J}{\partial y}=W_{y, a} * \frac{\partial J}{\partial y}+\frac{\partial J}{\partial a_{t+1}}$$
$$\frac{\partial J}{\partial a_{t+1}}=\frac{\partial J}{\partial \tanh (x, a)}=\left(1-a^2\right) * \frac{\partial J}{\partial a}$$
注:当$t=T$时,$\frac{\partial J}{\partial a_{t+1}}=0$;代码上,$\frac{\partial J}{\partial a_{t+1}}$是通过迭代$\frac{\partial J}{\partial a}$得到的;
误差来源于输出节点和下一时间步的隐藏节点;
隐藏层状态的权重和偏置的求导:
$$\frac{\partial J}{\partial W_{a, x}} =X * \frac{\partial J}{\partial \tanh (x, a)}$$
$$\frac{\partial J}{\partial W_{a, a}}=a_{t-1} * \frac{\partial J}{\partial \tanh (x, a)}$$
$$\frac{\partial J}{\partial b_a}=\frac{\partial J}{\partial \tanh (x, a)}$$
注:当$t=0$时,$a_{t-1}=0$
这边没体现出梯度累加的含义?
# 参考资料
- 循环神经网络(RNN):从0开始推导公式(全网步骤最全)_IT猿手的博客-CSDN博客 (opens new window)
- 手写RNN,并与官方RNN比较最终输出结果 - 知乎 (zhihu.com) (opens new window)
- Beginner’s Guide on Recurrent Neural Networks with PyTorch (floydhub.com) (opens new window)
- Why RNN needs two biases? - PyTorch Forums (opens new window)
# 工作流程
# 文献记录:数据处理?网络结构?
SPEAKER RECOGNITION WITH RECURRENT NEURAL NETWORKS
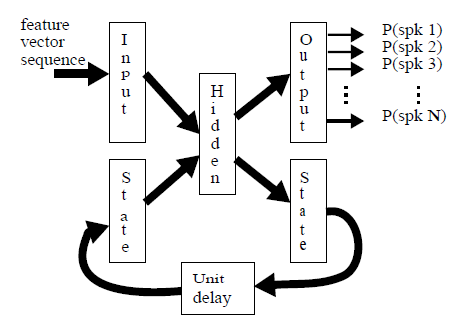
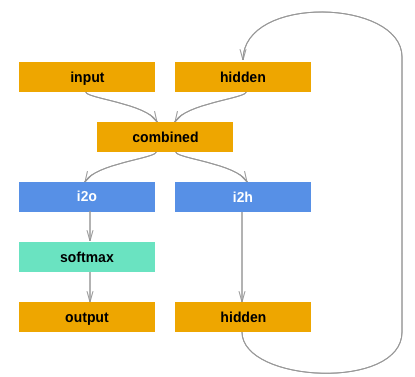
- 与传统RNN结构不尽相同:1)输入与隐藏层状态需同时输入网络;2)相邻时刻的隐藏层状态具有权重;
- 对一句话内所有帧的最后一个时间步输出取平均
- 30spks,3utts用于训练,3utts用于测试,固定短语“Assalam-o-Alaikum”
Deep Neural Network based Text-Dependent Speaker Recognition: Preliminary Results
- 在训练期间,DNN看到的标记数据点比RNN多得多;
- DNN通过将帧级的隐层输出进行平均化处理,得到语音级特征;
- RNN做法很多:
- 将每个时间步得到的隐层输出,对不同时间点赋予不同的权重
- 对所有时间步的隐层输出取平均
- 只取最后一个时间步的隐层输出
End-to-End Text-Dependent Speaker Verification
- RNN:只取最后一个时间步的输出【所以是隐层还是输出层?】
- “OK, Google”,大概可以分为80帧,0.6s左右
- DNN包含4个隐藏层,504个节点/层,
Locally connected and convolutional neural networks for small footprint speaker recognition
- 基于DNN减少模型参数等,以便用于移动端部署
- DNN的输入是选取左右帧,直接拼接后输入
- 每个人有几句话;每句话有几个输入样本;每个输入样本通过直接拼接语音帧得到;每句话通过对输入样本的最后一个隐藏层输出做平均,得到d-vector;一个说话人注册的时候有N句话,也就有N个d-vector;将N个d-vector取平均,得到该说话人模型
- 训练集:~745utts/spk,共3200utts;注册与测试集:3000spks,3~9utts/spk用于注册,7utts/spk用于验证
# 基于Pytorch的快速实现
# RNN VS DNN
语音特征提取
- 帧组的获取:
bin_size=30, step_size=10,分别去除前后一个帧组; - 对于固定长度的帧组,DNN取其统计量作为输入(1, 164),RNN直接将帧组作为时间序列输入(30, 41);
- 帧组特征都进行中心化
- 双层等宽DNN与单层RNN比较,隐藏层均为50个节点;
- 根据验证集准确率实时调整学习率,初始学习率均为0.01,衰减率为0.75;
- 最佳模型:最佳验证集准确率所对应的模型;
- 目前DNN与RNN使用的非线性激活函数均为$f=\tanh(x)$,后续需要调研光电实现;
- ❗权重初始化???
- 帧组的获取:
训练集、验证集及测试集的处理
- 30 frames/bin,10 frames/shift
- 确保训练集、验证集及测试集是一致的
- 如何保证DNN与RNN在shuffle后的帧组对应?【经验证,打乱后,标签是一致的】
- 打乱训练样本,不然网络只会对最后一个标签有强记忆
- 随机种子不是应用于speaker的,是应用于随机选择测试集语句的
RNN的输出应该是什么?所有时间步均值?最后一个时间步?时间步拼接?
⚠️实验证明,求均值才有好的结果,为何只用最后一个时间步不行?
| seed | DNN-1 layer | DNN-2 layers | RNN | DNN-1 layer | DNN-2 layers | RNN |
|---|---|---|---|---|---|---|
| 2 | 48.5015 | 47.3277 | 55.9441 | 93.3333 | 94.6667 | 100.0000 |
| 42 | 43.9703 | 44.4977 | 56.3654 | 90.0000 | 84.6667 | 100.0000 |
| 123 | 46.5563 | 46.0453 | 55.2933 | 89.3333 | 94.0000 | 100.0000 |
| 321 | 45.5938 | 45.1921 | 56.9671 | 86.6667 | 88.6667 | 100.0000 |
| 789 | 44.2331 | 41.3558 | 54.7671 | 86.0000 | 84.0000 | 98.0000 |
*执行脚本:mainDNN.py与mainRNN.py
# 结论
- 无论是bin acc还是utt acc,RNN > 单层DNN≈ 双层DNN
- RNN的实现中,有没有像DNN一样剔除前后帧组?有!
# 参考资料
- 基于pytorch实现RNN和LSTM对手写数字集分类的完整实例_Icy Hunter的博客-CSDN博客 (opens new window)
- pytorch学习-7:RNN 循环神经网络 (分类)_Paul-Huang的博客-CSDN博客_pytorch rnn 分类 (opens new window)
- PyTorch-Tutorial/402_RNN_classifier.py at master · MorvanZhou/PyTorch-Tutorial (github.com) (opens new window)
# 基于Numpy的RNN
弄清楚信号是怎么沿着时间轴传播的
| DNN | RNN | |
|---|---|---|
| 前向传播 | $\boldsymbol{a}^l=\sigma\left(\boldsymbol{W}^l \boldsymbol{a}^{l-1}+\boldsymbol{b}^l\right)$ | $\boldsymbol{h}^{(t)}=\sigma\left(\boldsymbol{z}^{(t)}\right)=\sigma\left(\boldsymbol{U} \boldsymbol{x}^{(t)}+\boldsymbol{W} \boldsymbol{h}^{(t-1)}+\boldsymbol{b}\right)$ |
| 反向传播 | 梯度沿着隐藏层数累加 | 梯度沿着隐藏层数和时间轴累加(BPTT) |
| 其他 | 权重矩阵初始化【正交处理】 梯度裁剪【梯度爆炸/梯度消失】 |
# RNN VS DNN
!!!Pytorch中RNN的激活函数只能是tanh,这里需要修改为sin【已修改】
如何保证公平的权重初始化?
| Seed | Net_type | 每轮打乱 | 帧组识别率 | 句子识别率 |
|---|---|---|---|---|
| 42 | DNN | √ | 47.7583 | 96.0000 |
| × | 44.5936 | 90.6667 | ||
| RNN | √ | 56.0297 | 100.00 | |
| × | 60.7049 | 100.0000 | ||
| 2 | DNN | √ | 50.9491 | 90.6667 |
| × | 47.7273 | 90.6667 | ||
| RNN | √ | 52.9471 | 98.0000 | |
| × | 60.0649 | 100.0000 |
*执行脚本:mainDNN_decoupled.py与mainRNN_decoupled.py
训练时,每一轮需要打乱样本吗?
- 对于DNN来说,打乱比较好;对RNN来说,不打乱比较好【为何这样?】;
- 无论是否打乱,RNN的效果都比DNN好
注:基本流程与Pytorch版本的一致,每轮迭代时,DNN打乱样本,RNN不打乱样本
| Seed | DNN-2 layers | RNN-1 layer | ||
|---|---|---|---|---|
| 2 | 50.9491 | 90.6667 | 60.0649 | 100.0000 |
| 42 | 47.7583 | 96.0000 | 60.7049 | 100.0000 |
# 注意事项
- 与基于Pytorch的实验结果不能吻合,第一个样本更新的权重完全能对应,但是第一轮样本迭代完就不行了。经排查,前几十个样本的权重更新都是没问题的,但是训练集有7500+的样本,精度导致的误差累积,使得一轮迭代后的梯度相差很大;
# 参考资料
- RNN的反向传播推导与numpy实现 - 知乎 (zhihu.com) (opens new window)
- 《神经网络的梯度推导与代码验证》之vanilla RNN的前向传播和反向梯度推导 - SumwaiLiu - 博客园 (cnblogs.com) (opens new window)【Tensorflow】
- 《神经网络的梯度推导与代码验证》之vanilla RNN前向和反向传播的代码验证 - SumwaiLiu - 博客园 (cnblogs.com) (opens new window)【Tensorflow】
- CaptainE/RNN-LSTM-in-numpy: Building a RNN and LSTM from scratch with NumPy. (github.com) (opens new window)
- 循环神经网络(RNN)模型与前向反向传播算法 - 刘建平Pinard - 博客园 (cnblogs.com) (opens new window)【推导更规范】
- Implementing a RNN with numpy | Quantdare (opens new window)
# 单层Fit-RNN的实现
- 权重初始化:RNN容易梯度消失,对初始权重进行正则化处理【还没弄,Pytorch是这样处理的吗?】
- Fit-DNN隐藏权重矩阵是变化的,Fit-RNN时间步之间共享同一个隐藏权重矩阵
- Fit-DNN只有第一个隐藏层需要输入层,Fit-RNN每个时间步都需要输入层
- 我们将$l$也用作RNN中的$t$
# Forward with local connection
- Fit-DNN:$h_n^{\ell}=e^{-\gamma \theta} h_{n-1}^l+\gamma^{-1}\left(1-e^{-\gamma \theta}\right) f\left(z_n^{\ell}\right)$,其中$h_n^{\ell}$来自于$z_n^{\ell}$与“上一时刻”的隐藏状态信号$h_{n-1}^{\ell}$;
- 对于Fit-RNN,$z_n^{t}$不仅来自于上一时刻的隐藏状态信号$h_{m}^{t-1}$,还来自于“当前时刻”的输入信号$I_t$;
- 怎么都是“上一时刻”呢?前一个上一时刻指的是DDEs的求解时间步,后面指的是信号输入的时间步(时序索引);
# BPTT with local connection
信号在单个虚拟节点中的传递
| Fit-DNN | Fit-RNN |
|---|---|
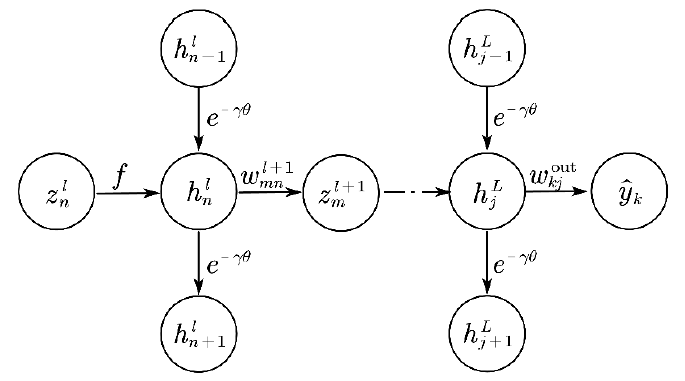 | 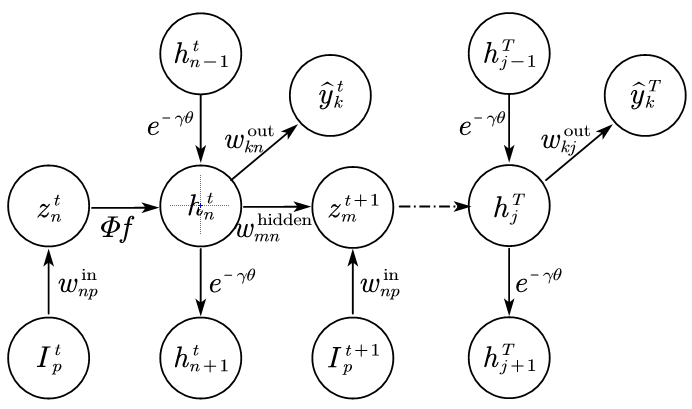 |
反向传播主要看把信号给了谁,误差就是由谁返回来的
BP with local connection
节点状态梯度:$\Delta_n^{\ell}=\frac{\partial \mathcal{L}}{\partial h_n^{\ell}}=\Delta_{n+1}^{\ell} e^{-\gamma \theta}+\sum_{i=1}^N \delta_i^{\ell+1} w_{i n}^{\ell+1}$
节点驱动信号梯度:$\delta_n^{\ell}=\frac{\partial \mathcal{L}}{\partial a_n^{\ell}}=\frac{\partial \mathcal{L}}{\partial h_n^{\ell}} \frac{\partial h_n^{\ell}}{\partial z_n^{\ell}}=\Delta_n^{\ell} \Phi f^{\prime}\left(z_n^{\ell}\right)$
权重梯度:$\frac{\partial \mathcal{L}}{\partial w_{n j}^{\ell}}=\frac{\partial \mathcal{L}}{\partial z_n^{\ell}} \frac{\partial z_n^{\ell}}{\partial w_{n j}^{\ell}}=\delta_n^{\ell} h_j^{\ell-1}$
Fit-RNN:$z_n^{t}$通过非线性函数把信号给了$h_n^{t}$;$h_n^{t}$通过隐藏权重把信号给了$z_n^{t+1}$,通过DDEs的耦合系数给了$h_{n+1}^{t}$
需要修改的部分:梯度沿时间轴累加
基本流程:先计算节点状态信号与节点驱动信号的误差,再计算权重矩阵的梯度
示意图有误,没有在非线性函数$f$前乘上系数[已修正]
# 参数确定[未完待续]
类似于Paper 1,考察Fit-RNN与RNN的等效性,并确定出最佳的虚拟节点间距与延迟环数量
# 虚拟节点间距
- 全连接状态下,考察$\theta=[2^{-5}, 2^{-4}, ..., 2^{4}, 2^{5}]$时,分别与帧组识别率和Margin的关系
- 确保Fit-RNN的初始权重与RNN的一致;
- 考察反向传播是否考虑局部连接的影响;
| 2 | 42 | 123 | 321 | 789 | Ave | |
|---|---|---|---|---|---|---|
| - | 85.4167 | 84.7098 | 80.2296 | 84.8070 | 85.0955 | 84.0517 |
| $2^{-5}$ | 58.0729 | 49.6652 | 44.3878 | 59.4022 | 62.0382 | 54.7132 |
| $2^{-4}$ | 72.6562 | 76.6741 | 69.3878 | 74.9689 | 77.1975 | 74.1769 |
| $2^{-3}$ | 80.8594 | 79.3527 | 78.1888 | 78.2067 | 76.8153 | 78.6846 |
| $2^{-2}$ | 80.0781 | 83.0357 | 79.7194 | 78.0822 | 86.6242 | 81.5079 |
| $2^{-1}$ | 83.8542 | 83.8170 | 79.0816 | 80.3238 | 86.3694 | 82.6892 |
| $2^{0}$ | 86.1979 | 83.9286 | 79.3367 | 82.9390 | 82.5478 | 82.99 |
| $2^{1}$ | 87.1094 | 86.1607 | 81.1224 | 83.4371 | 84.8408 | 84.5341 |
| $2^{2}$ | 85.8073 | 83.9286 | 82.2704 | 83.1880 | 86.3694 | 84.3127 |
| $2^{3}$ | 88.0208 | 85.4911 | 80.9949 | 84.6824 | 87.0064 | 85.2391 |
| $2^{4}$ | 86.0677 | 84.7098 | 81.5051 | 83.3126 | 87.5159 | 84.6222 |
| $2^{5}$ | 88.4115 | 83.7054 | 79.3367 | 82.0672 | 85.6051 | 83.82518 |
*执行脚本:mainRNN_decoupled.py和mainRNN_coupled.py
- 我们可以得出,最佳的$\theta=8$
| 2 | 42 | 123 | 321 | 789 | Ave | |
|---|---|---|---|---|---|---|
| - | 85.4167 | 84.7098 | 80.2296 | 84.8070 | 85.0955 | 84.0517 |
| $2^{-5}$ | ||||||
| $2^{-4}$ | ||||||
| $2^{-3}$ | ||||||
| $2^{-2}$ | ||||||
| $2^{-1}$ | ||||||
| $2^{0}$ | ||||||
| $2^{1}$ | ||||||
| $2^{2}$ | ||||||
| $2^{3}$ | ||||||
| $2^{4}$ | ||||||
| $2^{5}$ |
*执行脚本:mainRNN_decoupled.py和mainRNN_dde_heun.py
| 2 | 42 | 123 | 321 | 789 | Ave | |
|---|---|---|---|---|---|---|
| - | 85.4167 | 84.7098 | 80.2296 | 84.8070 | 85.0955 | 84.0517 |
| $2^{-5}$ | ||||||
| $2^{-4}$ | ||||||
| $2^{-3}$ | ||||||
| $2^{-2}$ | ||||||
| $2^{-1}$ | ||||||
| $2^{0}$ | ||||||
| $2^{1}$ | ||||||
| $2^{2}$ | ||||||
| $2^{3}$ | ||||||
| $2^{4}$ | ||||||
| $2^{5}$ |
*执行脚本:mainRNN_decoupled.py和mainRNN_dde_ibp.py
# 延迟环数
# 数值仿真[未完待续]
- 目的:证明Fit-RNN等价于RNN;
- 四种求解器的性能对比;
- 从TIMIT中随机抽取10个人进行实验验证;
| Solver | Description | Backprop | Bin acc[%] | Utt acc[%] |
|---|---|---|---|---|
| decoupled[RNN] | 经典神经网络 | classic | ||
| coupled | 在$[0,\theta]$区间内积分,求解步为$\theta$ 从第二层起,忽略$\theta$的一阶小量,直接使用第一层的迭代式 | node by node | ||
| dde_heun | 在$[0,\theta]$区间内积分,求解步$h=\theta/N_h$ 采用标准梯形规则通过半解析Heun法求解延迟微分方程 | node by node | ||
| dde_ibp | 在$[0,\theta]$区间内积分,求解步$h=\theta/N_h$ 采用分段积分的修正梯形规则的半解析Heun法求解延迟微分方程 | node by node |
*执行脚本:mainRNN_decoupled.py, mainRNN_coupled.py, mainRNN_dde_heun.py, mainRNN_dde_ibp.py
# Fit-DNN VS Fit-RNN
参数一览表
| DNN | RNN | |
|---|---|---|
| 输入预处理函数 | - | - |
| 非线性激活函数 | sin | sin |
| 输入层节点数 | 164 | 41 |
| 隐藏层节点数 | 50 | 50 |
| 隐藏层数 | 2 | 1 |
| 节点间距 | 4 | 4 |
| 延迟环数 | 99 | 99 |
实验结果
| seed | $\theta$ | bin acc(Fit-DNN) | utt acc(Fit-DNN) | bin acc(Fit-RNN) | utt acc(Fit-RNN) |
|---|---|---|---|---|---|
| 42 | - | 47.7583 | 96.0000 | 60.7049 | 100.0000 |
| 0.5 | 43.1791 | 89.3333 | 54.1117 | 96.0000 | |
| 2 | 48.2139 | 96.6667 | 56.8689 | 98.0000 | |
| 4 | 47.4706 | 92.0000 | 61.5680 | 100.0000 | |
| 8 | 47.2309 | 94.6667 | 61.6159 | 100.0000 | |
| 16 | 47.3268 | 94.6667 | 62.9825 | 100.0000 | |
| 2 | - | 50.9491 | 90.6667 | 60.0649 | 100.0000 |
| 2 | 48.4266 | 93.3333 | 60.6643 | 100.0000 | |
| 4 | 49.2008 | 92.6667 | 61.0140 | 100.0000 | |
| 8 | 48.7013 | 91.3333 | 60.7892 | 100.0000 | |
| 16 | 50.9491 | 90.6667 | 61.2637 | 100.0000 |
*执行脚本:mainDNN_coupled.py与mainRNN_coupled.py
# 结论
- Fit-RNN>Fit-DNN
- 与预期结论一样,当$\theta$较小时,求解速度比较快,但是效果略低于传统神经网络;反之,考虑到本地连接【间距越大不是影响越低吗?】,效果比传统的好
- ⚠️先前用tanh作为激活函数,效果不行,使得网络过拟合,具体原因以后再分析
- 使用别的求解器效果如何?
# ⭐三种折叠结构的对比
# Dynamic Reservoir Computing(DRC)
参考动态储油池计算原理及应用 (opens new window)这篇博客,DRC主要是利用系统的瞬态响应,动力系统的形式和参数并不是最重要的。因此,类似Fit-RNN,我们对Ikeda系统再做进一步的化简:$\dot{x}(t)=-x(t)+\eta \sin[x(t-\tau)+\zeta J(t)]$。同样地,类似于Fit-RNN系统,用常数变易公式得到迭代式:
$$X(t_n+h)=e^{-\alpha h}X(t_n)+(1-e^{-\alpha h})\eta\sin[x(t-\tau)+\zeta J(t)]$$
- $\zeta$类似于输入权重,可以与Fit-RNN做到统一;
- $\eta$是反馈增益,这是Fit-RNN/Fit-DNN中没有的,后期考虑加入看看效果;
- 对于分类任务,根据学位论文中的数值仿真结果,最佳实验参数配置为$\eta=0.3$,$\zeta=0.5$,$\phi=0.9\pi$
# 虚拟节点数
- 基于timit;
- 只用RC做粗略验证;
| N | Bin acc | Utt acc |
|---|---|---|
| 50 | 31.5512 | 60.0000 |
| 100 | 38.5759 | 74.0000 |
| 200 | 48.9331 | 92.0000 |
| 300 | 52.0499 | 96.0000 |
| 400 | 56.2455 | 98.0000 |
| 500 | 59.2184 | 98.0000 |
| 600 | 59.1465 | 100.0000 |
| 700 | 59.7938 | 100.0000 |
| 800 | 62.3591 | 100.0000 |
| 900 | 62.0714 | 100.0000 |
| 1000 | 63.5579 | 100.0000 |
| 没完了... |
- 完蛋了,这样的话,完美超过RNN,但我们对比的是折叠网络,还是得看Fit-RNN的性能表现;
- 但如果跟FitRNN一样只用50个节点,那必然没有优势;
- 那就公平点,50和200的实验都做,为什么不做400的,因为400的太慢了;
# 超参数配置
综上,DRC实验配置为$\eta=?$,$\zeta=?$,$\phi=?\pi$
# 🚩对比参数一览表
| DRC | Fit-DNN | Fit-RNN | |
|---|---|---|---|
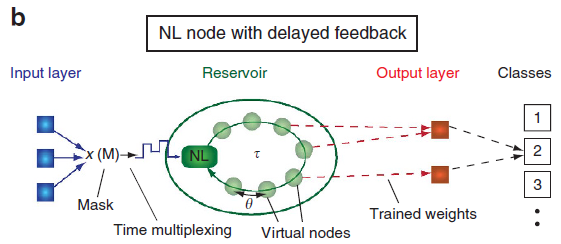 |  |  | |
| 介绍 | 对于一个具有nTimeStep的样本,可连续输入,时间步之间没有连接 | 系统对每个样本单独作响应,不可以连续输入 | 对于一个具有nTimeStep的样本,可连续输入,时间步之间具有连接 |
| 特征 | MFCC(dim=41) | MFCC_stats(dim=164) | MFCC(dim=41) |
| 单个样本长度 | bin | 以bin为单位计算统计量 | bin |
| 动力系统 | Ikeda | Ikeda | Ikeda |
| 求解器 | Heun法 | Heun法 | Heun法 |
| 延迟环数D | 1 | 99 | 99 |
| 虚拟节点数$N$ | 50 | 50 | 50 |
| 输入权重$W^{in}$ | 固定 | BP | BPTT |
| 隐藏权重$W^{hidden}$ | 固定 | BP | BPTT |
| 输出权重$W^{out}$ | 岭回归 | BP | BPTT |
| n_epoch | - | 50 | 50 |
| 初始学习率 | - | 0.01 | 0.01 |
- 根据动态储油池计算原理及应用 (opens new window)中Lyon耳蜗模型与MFCC的对比,选择使用MFCC;
- DNN-based计算帧组的统计量,RC/RNN-based直接输入帧组信号;
- 光电系统中,统一使用Ikeda动力系统,数值模拟采用常数变易公式推导;
- DRC不需要验证集,验证集是为了调节反向传播算法的更新率的,验证集并到训练集中;
- 如何确定虚拟节点间距?本文使用最佳Fit-RNN的参数配置;
- 初始学习率的确定:选为0.1时,RNN与Fit-RNN会出现nan和过拟合的问题;选为0.05时,RNN、DNN与Fit-DNN都无法正常运行,但Fit-RNN效果最好,相比于0.1能绝对提升6个点;综上,选择0.01;
# 说话人识别(TIMIT)
- 共50个说话人,男女平等,每人10条语音;
- 每条音频大概2~4s左右;
| $\theta=0.5$ | $\theta=8$ | $\theta=0.5$ | $\theta=8$ | ||
|---|---|---|---|---|---|
| Seed | Model | Bin acc | Bin acc | Utt acc | Utt acc |
| 2 | DRC | 32.0929 | 31.7183 | 68.0000 | 70.0000 |
| Fit-DNN | 43.2567 | 48.8511 | 86.0 | 92.0 | |
| Fit-RNN | 55.6444 | 60.614386 | 100.0 | 100.0 | |
| 42 | DRC | 33.6370 | 32.4383 | 66.0000 | 68.0000 |
| Fit-DNN | 43.1551 | 47.1590 | 92.0 | 96.0 | |
| Fit-RNN | 54.926876 | 56.605131 | 100.0 | 98.0 | |
| 123 | DRC | 33.1224 | 32.7330 | 68.0000 | 66.0000 |
| Fit-DNN | 44.9501 | 48.0896 | 90.6667 | 96.6667 | |
| Fit-RNN | 53.808713 | 58.165004 | 96.0 | 100.0 | |
| 321 | DRC | 33.3668 | 33.3919 | 70.0000 | 68.0000 |
| Fit-DNN | 43.1333 | 44.3887 | 91.3333 | 88.0 | |
| Fit-RNN | 56.942004 | 60.256088 | 100.0 | 100.0 | |
| 789 | DRC | 33.1870 | 32.4799 | 66.0000 | 62.0000 |
| Fit-DNN | 40.8193 | 42.9407 | 85.3333 | 82.0 | |
| Fit-RNN | 56.400878 | 58.327237 | 100.0 | 98.0 | |
| Ave | DRC | 33.0812 | 32.5523 | 67.6 | 66.8 |
| Fit-DNN | 43.0629 | 46.2858 | 89.0667 | 90.9333 | |
| Fit-RNN | 55.5446 | 58.7936 | 99.2 | 99.2 |
脚本:
mainFitDNN.py,mainFitRNN.py,mainDRC.py,mainRC.py补充节点数为200的实验,此时学习率为0.005,因为0.01的情况下,运行不下;
延迟环数均为99,当RNN为全连接时,跑不下去;
一个Fit-RNN算例需要8个小时!
| $\theta=0.5$ | $\theta=8$ | $\theta=0.5$ | $\theta=8$ | ||
|---|---|---|---|---|---|
| Seed | Model | Bin acc | Bin acc | Utt acc | Utt acc |
| 2 | DRC | 51.3736 | 51.3736 | 94.0000 | 94.0000 |
| Fit-DNN | 51.1489 | 55.9191 | 94.6667 | 94.6667 | |
| Fit-RNN | 58.7912 | 62.5874 | 100.0000 | 100.0000 | |
| 42 | DRC | 51.7382 | 51.3786 | 90.0000 | 96.0000 |
| Fit-DNN | 50.5394 | 53.5123 | 98.0000 | 98.6667 | |
| Fit-RNN | 59.7219 | 61.9516 | 100.0000 | 100.0000 | |
| 123 | DRC | 51.3994 | 51.4480 | 96.0000 | 94.0000 |
| Fit-DNN | 50.4746 | 53.7114 | 98.0000 | 94.0000 | |
| Fit-RNN | 59.7956 | 61.7425 | 100.0000 | 100.0000 | |
| 321 | DRC | 54.5318 | 54.2305 | 96.0000 | 98.0000 |
| Fit-DNN | 51.6696 | 52.4981 | 92.6667 | 96.0000 | |
| Fit-RNN | 59.7037 | 66.8592 | 100.0000 | 100.0000 | |
| 789 | DRC | 50.2804 | 50.1829 | 92.0000 | 94.0000 |
| Fit-DNN | 47.5738 | 50.1829 | 90.6667 | 90.6667 | |
| Fit-RNN | 59.1563 | 63.9844 | 100.0000 | 100.0000 | |
| Ave | DRC | 51.8647 | 51.7227 | 93.6 | 95.2 |
| Fit-DNN | 50.2813 | 53.1648 | 94.8 | 94.8 | |
| Fit-RNN | 59.4337 | 63.4250 | 100.0 | 100.0 |
# 口述数字识别(FSDD)
- 0~9数字,共有6个说话人的声音;
- 每条音频大概0.5s;
- 先进行节点间距$\theta=0.5$的实验:
| Seed | Model | $N=50$ | $N=200$ |
|---|---|---|---|
| 2 | DRC | 87.8889 | 98.7778 |
| Fit-DNN | 96.6667 | 97.2222 | |
| Fit-RNN | 95.0000 | 95.1111 | |
| 42 | DRC | 89.1111 | 98.6667 |
| Fit-DNN | 95.5556 | 96.5556 | |
| Fit-RNN | 96.6667 | 97.1111 [没能生成结果文件] | |
| 123 | DRC | 87.8889 | 98.0000 |
| Fit-DNN | 96.7778 | 96.6667 | |
| Fit-RNN | 96.3333 | 94.2222 | |
| 321 | DRC | 89.0000 | 98.6667 |
| Fit-DNN | 96.6667 | 96.7778 | |
| Fit-RNN | 96.3333 | 96.7778 | |
| 789 | DRC | 88.3333 | 98.0000 |
| Fit-DNN | 97.1111 | 97.3333 | |
| Fit-RNN | 95.2222 | 96.4444 | |
| Ave | DRC | 88.4444 | 98.4222 |
| Fit-DNN | 96.5556 | 96.9111 | |
| Fit-RNN | 95.9111 |
- 再进行$\theta=8$的实验
| Seed | Model | $N=50$ | $N=200$ |
|---|---|---|---|
| 2 | DRC | 88.2222 | 98.8889 |
| Fit-DNN | 96.1111 | 97.4444 | |
| Fit-RNN | 97.5556 | 97.8889 | |
| 42 | DRC | 89.5556 | 98.5556 |
| Fit-DNN | 97.6667 | 96.5556 | |
| Fit-RNN | 97.1111 | ||
| 123 | DRC | 87.8889 | 98.1111 |
| Fit-DNN | 97.2222 | 97.7778 | |
| Fit-RNN | 97.2222 | 97.7778 | |
| 321 | DRC | 89.1111 | 98.3333 |
| Fit-DNN | 97.1111 | 97.4444 | |
| Fit-RNN | 96.5556 | 97.4444 | |
| 789 | DRC | 89.0000 | 98.2222 |
| Fit-DNN | 97.4444 | 97.1111 | |
| Fit-RNN | 97.4444 | 97.7778 | |
| Ave | DRC | 88.7556 | 98.4222 |
| Fit-DNN | 97.1111 | 97.2667 | |
| Fit-RNN | 97.1778 |
# 反馈增益[未完待续]
# 参考资料
# 其他
- 为什么RNN不是将上一时刻的隐藏驱动信号给当前时刻的隐藏驱动信号?或者上一时刻的隐藏状态信号给当前时刻的隐藏状态信号?为什么是上一时刻的隐藏状态信号给当前时刻的隐藏驱动信号?
- ⚠️为什么DRC需要预热阶段,Fit-DNN/Fit-RNN不需要呢?
