 动力系统相关分析
动力系统相关分析
为什么Fit-DNN的识别性能高于DRC?本文试着从动力系统角度给出分析。相比于DRC,Fit-DNN有了更多的延迟环,且都带有反馈模块,动力系统处理信息的能力(IPC)会因此变强吗?
我们基于NARMA10任务考察IPC,因为该任务需要线性与非线性信息处理能力,考察得比较全面。
# 动力系统
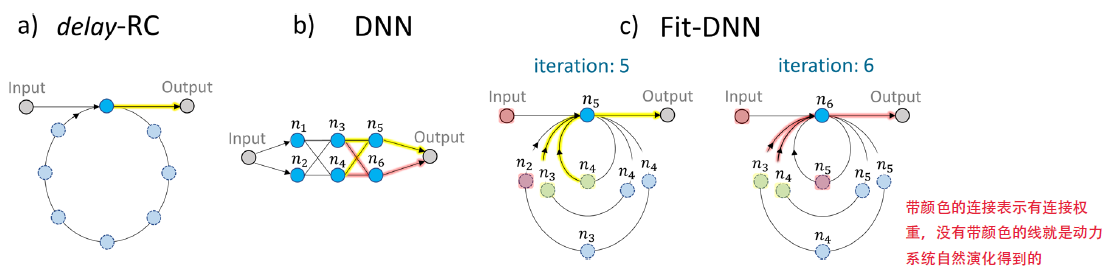
| 系统 | 表达式 | 类型 |
|---|---|---|
| DRC(Ikeda) | $\dot{x}(t)=-x(t)+\eta \sin ^2[x(t-\tau)+\gamma J(t)+\phi]$ | 定常延迟 |
| DRC(Mackey – Glass) | $\dot{X}(t)=-X(t)+\frac{\eta \cdot[X(t-\tau)+\gamma \cdot J(t)]}{1+[X(t-\tau)+\gamma \cdot J(t)]^p}$ | |
| Fit* | $\begin{gathered} \dot{h}(t)=-\gamma h(t)+f(z(t)) \ z(t)=I(t)+b(t)+\sum_{d=1}^D G_d(t) h\left(t-\tau_d\right) \end{gathered}$ | 有限时间下的时变延迟 |
RC中只考虑节点状态得到的输出权重,使得预测值与目标值有一个稳定的偏移,是不是该加个偏置?
应该添加,若状态矩阵为(节点数, 时间步),在最后一行加上元素均为1的行向量
正态分布的信号从哪里输入,从输入权重之前还是之后?
输入权重之前
为什么DRC有预热阶段,Fit-DNN并不需要?
Fit-DNN到底属于什么动力系统?
每一时刻都接收一种不同长度的延迟,这个延迟是与时间/状态无关的常数;
延迟每一时刻都在变化,属于time-varying/dependent delay;
这个动力系统是有时间范围的,能分析吗?
原作者团队表示,分析起来比较复杂,暂时没有相关文献
JiTCDDE可以分析time-varying/dependent delay
为什么DRC的反馈增益在非线性函数外面,Fit*在非线性函数里面?
# 时间序列预测NARMA10
NARMA10系统常用于测试ESN模型,因为它既需要非线性变换,也需要记忆能力,这是RC系统的主要特点。NARMA10系统的输出:
$$y(t+1)=0.3 y(t)+0.05 y(t)\left(\sum_{i=1}^9 y(t-i)\right)+1.5 u(t-9) u(t)+0.1$$
其中,$u(t)$是在时间步$t$的随机输入,从均匀分布$[0, 0.5]$中抽样,$y(t)$即为相应的输出。我们训练输出权重,使得ESN可以从储油层状态和$u(t)$预测出$y(t+1)$。
DNN只能处理离散时间,怎么实现NARMA10时间序列预测任务呢? 只能说Fit-DNN对于过去时刻的信息,存储在虚拟节点中,因此每次都只平移一个
ESN如何划分训练集与测试集?
# Get Data data, Y = NARMA10.getData(train_cycles+test_cycles) # 除去了前1000个点 data_train, Y_train = data[:train_cycles], Y[:train_cycles] data, Y = NARMA10.getData(train_cycles+test_cycles) # 为什么要再生成一次? data_test, Y_test = data[train_cycles:], Y[train_cycles:] # Reservoir & Training # setup reservoir Echo = ESN.ESN(inSize, outSize, resSize, alpha) # get reservoir activations for training data RA_Train = Echo.reservoir(data_train) # caclulate output matrix via moore pensore pseudoinverse (linear reg) Wout = np.dot(np.linalg.pinv(RA_Train), Y_train ) # get reservoir activation for test data RA_Test = Echo.reservoir(data_test, new_start=True) # 没有延用trian中的历史状态 # calculate predictions using output matrix Yhat = np.dot(RA_Test, Wout) # Calculate Error # we throw away the first 50 values, cause the system needs # enough input to being able to predict the NARMA10, since it is a # delayed differential equation NRMSE = np.sqrt(np.divide( \ np.mean(np.square(Y_test[50:]-Yhat[50:])), \ np.var(Y_test[50:])))1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25NARMA10.getData的关键代码:# generate input u = 0.5 * np.random.uniform(low=0.0, high=1.0, size=(N+1000)) # generate output arrays y_base = np.zeros(shape=(N+1000)) # 前面增加1000个点 y = np.zeros(shape=(N, Lag+1)) # calculate intermediate output for i in range(10, N+1000): # implementation of a tenth order system model y_base[i] = 0.3 * y_base[i-1] + 0.05 * y_base[i-1] * \ np.sum(y_base[i-10:i]) + 1.5 * u[i-1] * u[i-10] + 0.1 # throw away the first 1000 values (random number), since we need # to allow the system to "warm up" # 所以说ESN的前1000个点不算数,NARMA10相应的部分也不算数 u = u[1000:]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17ESN状态更新:
# 为什么没有启动部分? for t in range(data.shape[0]): u = data[t] # initialize input at timestep t # generate new reservoir state self.R = (1 - self.alpha)*self.R + \ self.alpha*np.tanh( np.dot( np.hstack((1,u)), self.Win) + \ np.dot(self.R, self.W)) # 将偏置、输入及状态存放在一行内 self.dm[t] = np.append(np.append(1,u), self.R)1
2
3
4
5
6
7
8
9
10
11
# 信息处理容量(IPC)
我们演示了如何量化这些系统可以处理信息的不同模式,并将它们结合起来定义动态系统的计算能力。这是由动态系统的线性独立状态变量的数量限制的,如果系统服从衰落记忆条件,则等于线性独立状态变量的数量。它可以被解释为系统可以计算的其刺激的线性无关函数的总数。通过逻辑映射、递归神经网络和二维反应扩散系统的数值模拟来说明我们的理论,揭示了计算的非线性和系统的短期记忆之间的普遍权衡。
Dambre等人引入的与任务无关的信息处理容量(Information Processing Capacity, IPC)决定了动态系统如何记忆先前的输入以及如何进一步转换它们。将系统状态分解为正交基来测量系统中处理和保存的输入历史的类型和数量。
将目标输出用有限个归一化后的多项式的乘积表示:
$$y_{\left{d_i\right}}=\prod_i \mathcal{P}_{d_i}(u(t-i))$$
可以得到不同阶次的IPC含量(线性,二次,三次...):
$$C_{T O T}[C]=\sum_{\left{d_i\right}} C_T^\epsilon\left(X,\left{d_i\right}\right)$$
IPC方向文章最多的是Felix Köster,Fit-DNN的通讯作者也曾是他的通讯作者
参考文献:
- Kubota, T., et al. (2021). "Unifying framework for information processing in stochastically driven dynamical systems." Physical Review Research 3(4): 043135.
- Dambre, J., et al. (2012). "Information Processing Capacity of Dynamical Systems." Scientific Reports 2(1): 514.
参考代码:kubota0130/ipc (github.com) (opens new window)

# 关键思想
基本框架(代码实现)
目标多项式$z_t^{(i)}$属于多元多项式,可以表示为多个一元多项式之积,这里的“元”表示延迟信号:
$$z_t^{(i)}=\prod_{s=1}^{\infty} \mathcal{F}{n_s^{(i)}}\left(\zeta{t-s}\right)$$
其中,$i$表示某一种${[[n, s]]}$所在的索引,如上图所示
对于状态信号$X$,其第$i$个${[[n, s]]}$对应的IPC定义:
$$C(X,\boldsymbol{z}^{(i)})=\frac{\boldsymbol{z}^{(i) \top} \boldsymbol{X} \boldsymbol{X}^{+} \boldsymbol{z}^{(i)}}{\boldsymbol{z}^{(i) \top} \boldsymbol{z}^{(i)}}$$
其中,$\boldsymbol{X}^{+}$表示$\boldsymbol{X}$的伪逆
对状态信号$X$去均值(沿时间轴)后,进行SVD分解,得到线性独立、正交化后的状态向量$P$:
$$X=P \Sigma Q^{\top}$$
其中,$X$的尺寸为$(T,N)$,$P$的尺寸为$(T,R)$,$\Sigma$的尺寸为$(R,R)$,是包含了奇异值的对角矩阵
对目标多项式进行归一化,得到$\phi^{(i)}=z^{(i)} /\left|z^{(i)}\right|$,由此IPC可以转化为:
$$C\left(\boldsymbol{X}, z^{(i)}\right) =\frac{z^{(i) \top}}{\left|z^{(i)}\right|} \boldsymbol{P} \boldsymbol{P}^{\top} \frac{z^{(i)}}{\left|z^{(i)}\right|} =\left|\boldsymbol{P}^{\top} \boldsymbol{\phi}^{(i)}\right|^2$$
总容量应该为所分析信号的矩阵秩,因此,状态矩阵的rank为节点数,同样的,输出的rank为1,因为是一维信号
论文创新
同时,状态矩阵$X$可以由目标多项式$z_t^{(i)}$通过混沌多项式展开:
$$\boldsymbol{x}t=\sum{i=1}^{\infty} c_i z_t^{(i)}$$
将目标多项式转换为归一化多项式,得到状态矩阵表达式:
$$\boldsymbol{x}t=\sum{i=1}^{\infty} \phi_t^{(i)} \hat{\boldsymbol{c}}_{\boldsymbol{i}}$$
可以得到:$X=\sum_{i=1}^{\infty} \phi^{(i)} \cdot \hat{c}_i^{\top}=\lim _{M \rightarrow \infty} \Phi \hat{C}^{\top}$,【没太理解$M$的意思,是最值吗?比如前$M$个最大的奇异值?】
同样地,对状态矩阵进行SVD分解,得到:
$$\boldsymbol{P}=\lim _{M \rightarrow \infty} \boldsymbol{\Phi} \boldsymbol{\Lambda}^{\top}$$
其中,$\boldsymbol{\Lambda}=\left[\lambda_1 \cdots \lambda_M\right]=\boldsymbol{\Sigma}^{-1} \boldsymbol{Q}^{\top} \hat{\boldsymbol{C}}$是常数矩阵
因此,IPC可以写为:$C\left(\boldsymbol{X}, z^{(i)}\right) = |\lambda_{i}|^2$
综上所述,$i$-th ${[[n, s]]}$对应的IPC等于混沌多项式展开(Polynomial chaos expansion, PCE)后基的系数向量的平方范数
# 代码实现细节
尽管文献验证了$i$-th ${[[n, s]]}$对应的IPC等于混沌多项式展开(Polynomial chaos expansion, PCE)后基的系数向量的平方范数,但代码中展示的是传统IPC计算方式,足矣!
符号申明
- ${[d, s_{max}]}$:${[2, 300], [5, 15]}$表示指定了两个degree,及对应的最大延迟
- ${[[n]]}$:以$[5,15]$为例,该符号表示所有可能的$n$排列,ex. {[[3, 1, 1],[2, 1, 1, 1],[3, 2]..., [5]]}
- ${[[n, s]]}$:在指定${[[n]]}$下,对应安排合适的延迟,ex. {[[3, 10], [1, 5], [1, 3]],[[2, 8], [1, 4], [1, 2], [1, 1]],[[3, 11], [2, 7]], ..., [[5, 5]]}
具体步骤
指定需要考察的合集:${[d, s_{max}]}$,$s_{max}$应随着$d$的增加而减少;
指定PC多项式类型和输入信号的分布,文献中提供了8种常见分布及随机分布;
实例化IPC
输入信号$u$必须严格对应多项式类型,本研究使用对称输入,范围[-1, 1];
根据$d_{max}$,$u$及多项式类型,得到一元多项式,并进行归一化【后续对多元多项式还需要进行归一化】;
实例化集合${[[n, s]]}$
计算得到动力系统的状态矩阵$X$,尺寸:[节点数,时间步]
- 时间步包含了预热阶段;
- 训练输出权重或者是评估NMSE性能时,去除预热时间;
对$X$进行SVD分解(注:代码中对文献中的$X$进行了转置)
- 中心化:沿时间轴去均值,并去除预热时间;
- SVD分解:得到秩(用于验证IPC)、一组线性独立且正交的状态向量$P$;
对于每一个$[d, s_{max}]$,计算IPC
- 筛选出满足$[d, s_{max}]$的所有${[[n, s]]}$
- 根据$d$,得到合适的${[[n]]}$,其长度不能超过$s_{max}$,并排序;
- 对每一种${[[n]]}$,安排合适的$s$进行搭配,并排序;
- 得到每一种${[[n, s]]}$在${[[n]]}$中的位置索引,用于后续IPC截断;
- 对于每一个${[[n, s]]}$:
- 根据${[[n, s]]}$,得到目标多项式,为对应的一元多项式之积;
- 计算对应的IPC分量,包括目标多项式的归一化;
- 筛选出满足$[d, s_{max}]$的所有${[[n, s]]}$
对较小的IPC分量进行截断
- 对于所有$n$的排列,随机选择一组对应的$s$组成${[[n, s]]}_{shuffle}$,假设有5组;
- 打乱输入信号$\zeta$,执行200次,得到200条打乱后的输入信号$\zeta_{shuffle}$;
- 计算得到$IPCs_{shuffle}$,尺寸为$(5, 200)$;
- 找出每一组${[n, *]}{shuffle}$对应的最大IPC,得到$IPC{max}$,尺寸为$(5, 1)$;
- 指定$th_{scale}=1.2$, 得到每一组${[n, *]}$的阈值$th_{scale}*IPC_{max}$;
- 对于每一组${[[n, s]]}$,根据步骤6中得到的位置索引,判断IPC分量是否大于阈值,不足则记为0;
统计截断后的IPC分量
# ⭐疑问
Task 2中,为什么IPC实例化使用的是对称输入,ESN使用的是非对称输入?
对于ESN来说,对称输入只能得到奇数阶容量,为了得到二阶记忆容量,我们将非对称输入应用于ESN;【但这个时候应该就不能分析目标输出了】
Task 3中,为什么IPC和ESN中使用的是对称输入,NARMA10任务使用的是非对称输入?ESN的输入信号不应该跟NARMA10对齐吗?
在Github的issue中,作者表示,PC需要[-1, 1]范围内的均匀分布以构造正交的目标多项式。如果使用[0, 1]的话,多项式重叠,导致总容量大于其上限。因此,IPC的输入范围严格取决于对应的多项式。反之,ESN可以接收任何范围的输入信号。【如果IPC的输入不必与动力系统的统一,那凭什么可以分析目标输出呢?所以,动力系统也使用了[-1,1],那为啥动力系统的输入与NARMA10任务输入不统一,这样也行的吗?】
当ESN为对称输入时,这个动力系统只能处理奇数阶容量。
文献中表示,当NARMA10为对称输入时,目标输出只需要二阶容量,反之,需要一阶与二阶容量。
如何准备多元多项式?
本文中表示,根据Cameron-Martin定理,多元正交多项式预计是单变量正交多项式的乘积,这也是为什么医院多项式需要归一化的原因;
一元多项式的基矩阵尺寸为[d+1,Two+T],多元多项式的基矩阵尺寸为[d+1,T];
为什么对$X$进行SVD?
可能文献中在推导IPC与PCE的关系时,需要使用SVD,单纯IPC求解时,可以使用SVD后的状态矩阵,也可以不用;
不同多项式分析出来的IPCs都不一样,这个分析方法还可靠吗?
应该是可靠的,对于一种多项式分解,不同动力系统的IPCs占比趋势应该是相似的;
# 参考资料
- 关于可决系数R-Square - 乞力马扎罗的雪的文章 - 知乎 https://zhuanlan.zhihu.com/p/36642259
- 方差与协方差的关系_方差 协方差_ChingeWang的博客-CSDN博客 (opens new window)
- Here’s How to Use CuPy to Make Numpy Over 10X Faster | by George Seif | Towards Data Science (opens new window)
- Information Processing Capacity | ipc (kubota0130.github.io) (opens new window)
# IPC分析
# 基于NARMA10任务的模型
相关代码已上传至ZhouWenjun2019/NARMA_DNN_RNN_RC (github.com) (opens new window)
# DNN-based
DNN的输入与输出应该如何准备?
一些参考项目
| 项目 | 描述 |
|---|---|
| [Time_Series/Forecasting Using DNN.ipynb at master · amitguptapc/Time_Series (github.com)](https://github.com/amitguptapc/Time_Series/blob/master/Forecasting Using DNN.ipynb) | 将训练集时间序列按照一定窗长分割,重新打乱顺序后作为数据集 |
| sherlockjian/Sunspots-Time-Series-Data-Prediction-using-DNN-s-and-LSTM-s (github.com) (opens new window) | 输出是保留了前面几个target的 |
| quyenvuong/Time-Series-in-Deep-Learning: The open price of AAL stock is collected up to Feb 2018. (github.com) (opens new window) | 股票预测,输出一维,隐藏层节点为10 |
DNN的节点数到底该如何设置?
应该确保有相同的虚拟节点数就可以了,输出权重可能会尺寸不一致,那状态矩阵还有意义吗?
DNN的性能不如RC,还有调试空间吗?DNN的NMSE在0.2左右,RC的NMSE在0.15左右
打乱训练集:没效果
自适应学习率:没效果
更改隐藏层节点数:没效果
固定随机种子:没效果
多维输出:性能下降至0.23
🚩增加输入维数至20:性能明显提升,测试输入维数对结果的影响
Seed Input nodes [1e3,1e4] [1e3,1e6] 42 10 0.212804 11 0.090854 15 0.042301 20 0.063821 123 10 0.208626 11 0.093704 15 0.044634 20 0.041315 注:执行脚本
ipc/NARMA_DNN.py,训练迭代次数为50,NMSE结果均为测试集结果;真的很神奇,为什么DNN不能只用10个输入节点,仅多一个节点,性能都有大幅提升,且优于RC很多;
# RNN-based
RNN的数据集如何准备?状态变量要持续使用吗?测试阶段的时间步必须与训练阶段一致吗?
项目 备注 AbishekNP/TimeSeries: Google stock price prediction using RNN (github.com) (opens new window) 训练与测试阶段皆以60个时间步为输入,输出一个预测值 geekquad/Time-Series-Prediction-from-Scratch (github.com) (opens new window) 输入20个点,输出为输入向后平移一个点,也是20个
训练阶段,状态变量是持续的
没有测试阶段RyanLBuchanan/Time_Series_Prediction_RNN (github.com) (opens new window) 测试阶段,只预测了一个值... 目前RNN基本框架只能实现
NMSE=0.3,甚至比DNN效果都差,做出一些尝试:每个阶段的状态变量持续使用:性能明显提升至0.17
增加样本的时间步至20:性能明显下降至0.34
🚩回退时间步为10, 一维输出:性能明显提升,比RC优秀很多,为 0.0629
同样的,查看输入时间步对性能的影响:
Seed Time steps NMSE 10 0.0731 11 0.0612 15 0.0759 20 0.072 不同于DNN,性能并不是随着时间步而提升的,但是11是最合适的步长;
# DRC-based
参考文献:Appeltant, L. (2012). Reservoir computing based on delay-dynamical systems.
论文中的最佳配置:
电子实现(Mackey – Glass):反馈增益$\eta=0.5$, 输入缩放因子$\gamma=0.05$,非线性阶数$p=1$, 虚拟节点间距$\theta=0.2$;(文献3.3.1.1)
光电实现(Ikeda):反馈增益$\eta=1.1$,输入缩放因子 $\gamma=0.01$,非线性相位$\phi=\pi/10$,虚拟节点间距 $\theta=0.2$;(文献4.3.1.1)
为了与IPC分析匹配,预热时间步与总时间步分别为[1e3, 1e6];
为什么MG与Ikeda得到的效果比传统RC差很多?
MG-based Ikeda-based 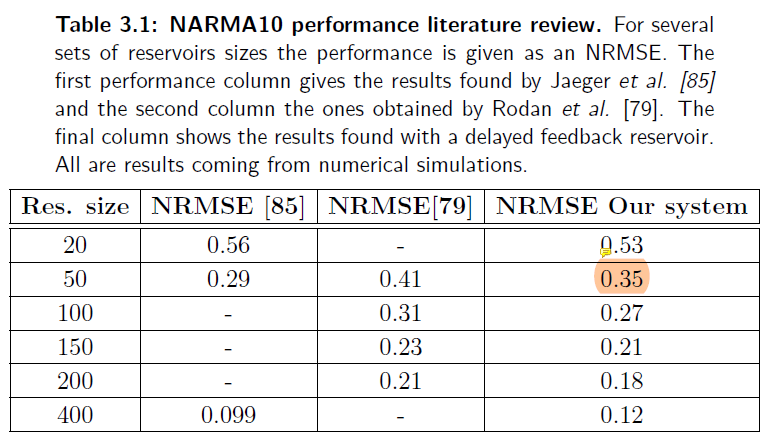
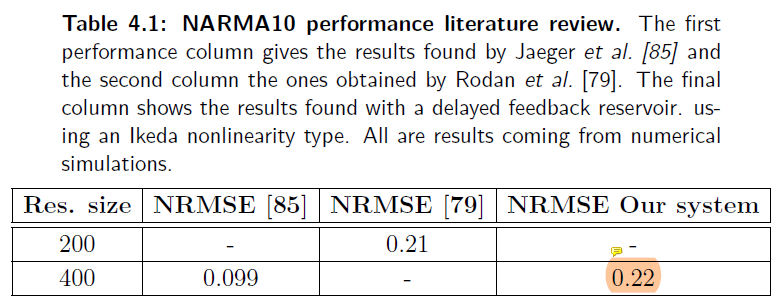
- 本研究只使用50个虚拟节点;
- MG的NMSE随着节点数增加而增加,而Ikeda可能过于简单,增加节点也无济于事;
当使用
Githubs/dynamic/DRC/Narma10-System-Identification中的输出权重训练时,当虚拟节点数为400,序列长度为1e6,其他设置同上时,NMSE=0.063397,当使用pinv法训练时,NMSE=0.247992;当虚拟节点数改为50时,使用迭代训练得到的NMSE=0.367073,pinv法得到的NMSE=0.573094;自己确定超参数
输入缩放因子暂定为0.01,遍例搜索反馈增益$[0,2]$与非线性相位$[0,\pi]$;
NMSE为训练集结果
$0.1\pi$ $0.2\pi$ $0.4\pi$ $0.6\pi$ $0.7\pi$ $0.8\pi$ $\pi$ 0.3 0.620721 0.5 0.612135 0.640340 0.635800 0.633017 0.999940 0.8 0.626283 1.0 0.664409 1.3 0.614257 1.4 0.646709 0.598533 0.744798 0.755157 0.710251 0.600717 0.999927 1.5 0.599296 2.0 0.970298 反馈增益定为1.4,非线性参数定为$0.2\pi$,现在调试输入缩放因子
0.001 0.005 0.01 0.05 0.1 0.5 0.610638 0.598190 0.598533 0.603718 0.612759 0.685615 综上:反馈增益为1.4,非线性参数为$0.2\pi$,输入缩放因子为0.005
# 性能对比
综合Fit-DNN、Fit-RNN及DRC的表现,使用以下配置:
迭代次数调整为50,初始学习率设置为0.01,虚拟节点间距设置为0.2;
DNN/RNN的输入样本维度均为11【这里有很大的问题,每个时间步应该只能输入一个样本点,需要重做实验!】;
输出权重统一用线性回归训练【其实没有必要,只要确保输入权重与输出权重均没有添加非线性函数即可!】;
| Net | train_nmse | test_nmse |
|---|---|---|
| RC | 0.137282 | 0.138581 |
| DRC | 0.598190 | 0.599283 |
| DNN | 0.082245 | 0.081444 |
| Fit-DNN | 0.082202 | 0.081390 |
| RNN | 0.084049 | 0.083152 |
| Fit-RNN | 0.088356 | 0.087331 |
为什么RNN-based性能比DNN-based低?
重新做标准对比实验,见“出现问题,重做实验”部分。结论是,当只有一维输入一维输出时,DNN完全无法训练;
# IPC对比
# 代码调试日志
不需要为了得到更低的NARMA而调整模型超参数,本就是查看系统对不同非线性信息的处理能力;
分析目标输出IPC时,时间步对结果是有影响的,当Two=1e4,T=1e6时,总IPC≈0.99,因为秩为1,符合预期,但是当Two=1e3,T=1e4时,总IPC≈4.5,有问题;
No [Two, T] 1阶 2阶 3阶 4阶 5阶 总 1 1e3, 1e4 0.853558 0.1264605 0.0714746 0.0562917 0.1154292 1.2232136 2 1e3, 1e5 0.855577 0.1337794 0.0059657 0.0029430 0.0064402 1.0047049 3 1e3, 1e6 0.859237 0.1374583 0.0004211 0.0008556 0.0008556 0.9991645 4 1e4, 1e5 0.856340 0.1372815 0.0106263 0.0251498 0.0091149 1.0385127 5 1e4, 1e6 0.859314 0.1374932 0.0001423 0.0016969 0.0002898 0.9989362 6 1e4, 1e7 无法运行 - - - - - 执行脚本:
Github/dynamic/analysis/ipc/s3.py- IPC分析准确性:1<2<3,4<5,2<5;
- 时间步越长结果越准确,随着时间步的下降:1阶IPC减少,2阶IPC减少,3阶IPC增大,4阶IPC,5阶IPC,总IPC增大;
- 为了获得比较准确的IPC分析,需要:1)Two在总时长的占比较小;2)T的绝对基数要大,至少为1e5;
需要考虑零延迟(0-based delay)吗?当然需要了,当前信号对当前结果必然有贡献
[Two, T] 0 1阶 2阶 3阶 4阶 5阶 总 1e3, 1e5 √ 0.855577 0.1337794 0.0059657 0.0029430 0.0064402 1.0047049 × 0.855577 0.1336787 0.0058390 0.0025464 0.0077300 1.0053708 1e3, 1e6 √ 0.859237 0.1374583 0.0004211 0.0008556 0.0008556 0.9991645 × 0.859237 0.1374254 0.0004085 0.0007163 0.0007163 0.9987723 1e4, 1e6 √ 0.859314 0.1374932 0.0001423 0.0016969 0.0002898 0.9989362 × 0.859314 0.1374771 0.0001423 0.0015453 0.0001556 0.9986343 1e3, 1e6/2 √ 0.857508 0.1345042 0.0009496 0.0055936 0.0018756 1.0004308 执行脚本:
Github/dynamic/analysis/ipc/s3.py- 不考虑当前信号对IPC的影响的话,1阶IPC没有变化,其他IPC都变少了;
- 1e3, 1e5的5阶IPC还挺奇怪的;
- 还是需要考虑零延迟的影响的;
- 好奇怪,最后一组啥结果啊,4阶跟5阶太奇怪了;
对FitDNN进行IPC分析:
- 用训练集数据,这样才能保证足够的步长;
- FitDNN理论上不需要预热时间(待实验验证);
- 考虑到训练时间,与RC尽量保持一致,IPC精度等原因,选择
[1e3, 1e6]; - 训练得太慢了且容易过拟合,先把学习率换成0.001试试,可行;
- 使用的是decoupled版本,NMSE(test)=0.081933
DRC版本NARMA10
- 使用Ikeda系统,与FitDNN保持一致;
- 注意到
folded/mainDRC.py中,对每一个样本都进行了ESN的实例化,这是有必要的,因为对于分类任务,每个样本的时间步不同; - DRC如何处理时间序列预测任务?不同于分类任务,每个样本之间是独立的,本任务可以只实例化一次ESN,记录下每个时间步的状态信号;
- 当使用MG系统时,NMSE=0.481825,Ikeda系统的结果为0.617306,太拉跨了【这都算好的了】
FitRNN版本NARMA10
- 使用的是decoupled版本;
- 输入维度是1,序列长度为11;
- 运行得太慢了,这是为什么;
- 迭代30次,当学习率为0.001时,NMSE大约为0.08314,这也太拉了,当学习率为0.01时,结果为0.101458,更拉...
❌Cupy调试
跑最简单的测试组都报错out of memory,在主脚本开始前添加如下代码:
pool = cp.cuda.MemoryPool(cp.cuda.malloc_managed) cp.cuda.set_allocator(pool.malloc)1
2运算到4阶IPC时,程序就会被kill掉,CPU和内存几乎飙升,GPU使用率为0:重新从4阶IPC开始计算,可以计算,但是5阶又开始遇到同样的问题,在调用Cupy后添加如下代码:
cp.cuda.Stream.null.synchronize()1大意是等当前进程执行完成后再进行下一步,可以连续完成4阶与5阶的计算
很奇怪,重新计算1~5阶IPC时,又是到4阶IPC被kill,暂时无法解决...
验证加速效果,查看总时长,执行脚本:
ipc/s3.py及ipc_back/s3_compare.py阶数 IPC Numpy Cupy 1~3 目标输出 373.05 583.36 状态矩阵 实际输出 4~5 目标输出 583.01 报错 状态矩阵 实际输出 尝试分批处理数据,未果
# ESN对称输入实验结果
参数设置:
对于所有模型,预热时间与总时间分别为[1e3, 1e6];
总时间分配,训练集,验证集,测试集比例:[0.8, 0.1, 0.1];
NMSE为测试集结果,IPC分析在训练集上完成;
保证所有模型的输入信号一致;
折叠网络全部使用Ikeda模型;
不干预隐藏权重;
# 模型参数(待完善)
| 模型 | 输入权重 | 隐藏权重 | 输出权重 |
|---|---|---|---|
| RC | 掩码:[-1, 0, 1] 输入缩放因子0.005 | 服从[0,1]正态分布 反馈增益0.95 | 线性回归 |
| DRC | 掩码:[-1, 0, 1] 输入缩放因子0.005 | 反馈增益1.4 非线性相位$0.2\pi$ | 线性回归 |
| DNN | [-1,1]均匀分布 输入缩放因子0.01 | 线性回归 | |
| Fit-DNN | [-1,1]均匀分布 输入缩放因子0.01 | 线性回归 | |
| RNN | 线性回归 | ||
| Fit-RNN | 线性回归 |
# 输出分析
| 1阶 | 2阶 | 3阶 | 4阶 | 5阶 | 总 | |
|---|---|---|---|---|---|---|
| RC | 0.994286 | 0.000193 | 0.000235 | 0.000243 | 0.000874 | 0.995831 |
| 百分比 | 100 | |||||
| DRC | 0.992363 | 0.003034 | 0.000236 | 0.002024 | 0.000361 | 0.998018 |
| 百分比 | 100 | |||||
| DNN | 0.866530 | 0.130377 | 0.000497 | 0.003340 | 0.002022 | 1.002766 |
| 百分比 | 100 | |||||
| Fit-DNN | 0.866488 | 0.130475 | 0.000449 | 0.003373 | 0.002073 | 1.002857 |
| 百分比 | 86.4019 | 13.010329 | 0.447721 | 0.336339 | 0.206709 | 100 |
| RNN | ||||||
| 百分比 | 100 | |||||
| Fit-RNN | 0.865795 | 0.129974 | 0.001161 | 0.003168 | 0.002242 | 1.002339 |
| 百分比 | 100 | |||||
| 目标输出 | 0.857826 | 0.136669 | 0.000324 | 0.001931 | 0.001346 | 0.998096 |
| 目标百分比 | 85.9462 | 13.6930 | 0.032461 | 0.193468 | 0.134857 | 100 |
# 状态矩阵分析
| 1阶 | 2阶 | 3阶 | 4阶 | 5阶 | 总 | |
|---|---|---|---|---|---|---|
| RC | 37.387471 | 0.0 | 12.753209 | 0.050009 | 0.019265 | 50.209954 |
| 100 | ||||||
| DRC | 8.877392 | 7.571017 | 0.028850 | 0.114107 | 0.038061 | 16.629428 |
| 100 | ||||||
| DNN | 10.991455 | 20.671975 | 18.254382 | 0.358666 | 0.358665 | 50.525164 |
| 100 | ||||||
| Fit-DNN | 10.993051 | 21.122077 | 17.462259 | 0.500057 | 0.215112 | 50.292556 |
| 100 | ||||||
| RNN | 10.875729 | 25.991555 | 10.961228 | 2.073252 | 0.533464 | 50.435228 |
| 100 | ||||||
| Fit-RNN | 6.716898 | 16.431264 | 19.618004 | 6.567806 | 0.912891 | 50.246864 |
| 100 |
- 为什么Fit-RNN差异这么大呢!3~5阶大幅上升;
- RC与DRC几乎没有二阶容量,是我使用了对称输入的原因,需要补充实验;
- DRC的状态矩阵容量很低,说明没有充分响应;
# 结果可视化
预计做两个堆叠柱状图,上面是状态矩阵分量{RC, DRC, RNN, Fit-RNN},下面是实际输出与目标输出分量{RC, DRC, RNN, Fit-RNN, target};
| 数值 | 柱状图 | |
|---|---|---|
| 状态矩阵 | 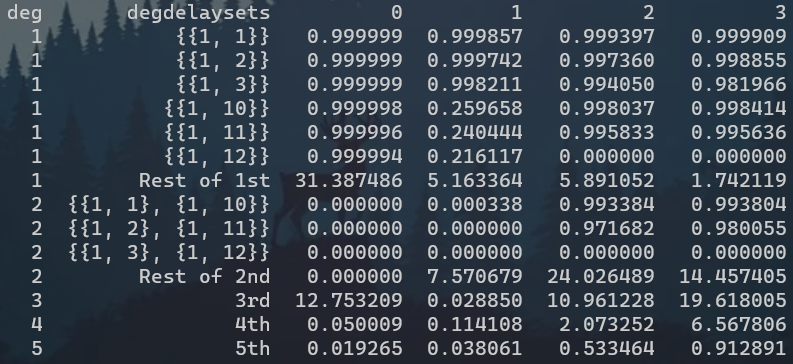 | |
| 实际/目标输出 | 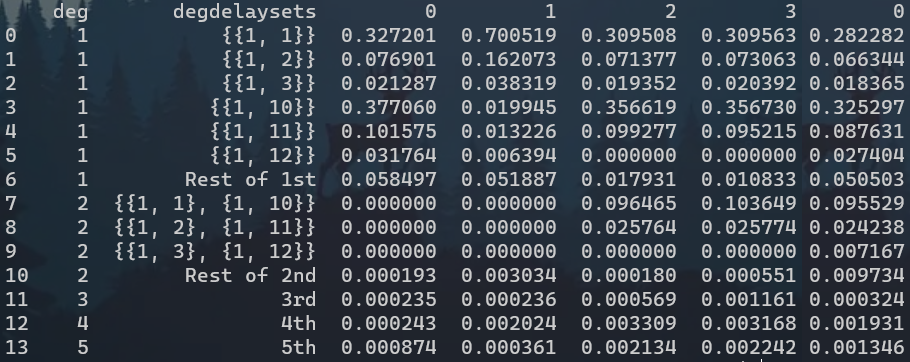 |
# 出现问题,重做实验
主要有两个问题:一是,应统一各模型每个时间步的输入样本为一维标量;二是,系统的输入应为[-1,1]的均匀分布,IPC的输入应与系统输入一致;
# Fit-RNN参数确定
DNN无法处理一维输入一维输出的问题,只对Fit-RNN做超参数确定;
取最后一个epoch的验证集NMSE;
| 0.1 | 0.01 | |
|---|---|---|
| Pytorch | 4.96979e-04 | 1.00956e-03 |
| decouple | 8.854396e-04 | 1.602110e-02 |
| 0.2 | 1.396104e-01 | 4.971426e-01 |
| 0.5 | 4.604675e-03 | |
| 1 | 2.114661e-03 | 2.314407e-01 |
| 8 | 1.414943e-03 | 1.635976e-02 |
| 16 | 1.710722e-03 | 1.630804e-02 |
当学习率为0.01且$\theta$取值很大时,每个epoch中,与decouple版本得到的nmse基本一致,但是到后面,梯度越来越小,耦合的影响还是变大了,偏差也逐渐变大;
当学习率为0.1且$\theta$取值很大时,decouple版本的学习率始终优于couple版本;
当学习率较大时,耦合带来的误差反向传播的影响变得不容忽视?确实如此,当$\theta=64$时,学习率0.1也可以得到完全一样的结果,该如何缩小节点间距呢?;
为什么Pytorch版本与decouple版本相差那么多呢?因为Pytorch版本只有tanh激活函数,而我们使用sin,当统一为tanh时,正向传播结果是一样的,反向传播有偏差;
综上,选择学习率为0.1,节点间距为0.5,说明与RNN差距的原因;
# 实验参数设置
- 虚拟节点间距设置为0.5;
- 在测试集上计算NMSE,在训练集上分析IPC;
- RNN-based
- 迭代次数为50,初始学习率为0.1,自适应学习率,衰减率为0.75;
- 训练阶段与测试阶段均使用
batch_size=10分批处理,实验证明,测试阶段,批处理与整条样本输入的结果是一致的,但批处理对计算机要求较小,采用批处理验证; - 假设一个batch有200个样本,反向传播会出现200个梯度,而w的梯度等于这两百个梯度求平均;
| 模型 | 输入权重 | 隐藏权重 | 输出权重 |
|---|---|---|---|
| RC | 服从[0,1]正态分布 输入缩放因子0.005 | 服从[0,1]正态分布 反馈增益0.95 | 线性回归 |
| DRC | 掩码:[-1, 0, 1] 输入缩放因子0.005 | 反馈增益1.4 非线性相位0.2\pi | 线性回归 |
| RNN | 用Pytorch默认初始化权重 | BPTT | 线性权重 |
| Fit-RNN | 用Pytorch默认初始化权重 | BPTT | 线性权重 |
# NMSE结果
经过初步测试,DNN-based在一维输入与一维输出的限制下,识别效果很差,不加入测试;
| Decoupled | Coupled | |
|---|---|---|
| RC | 0.13858082 | 0.59771093 |
| RNN | 8.4971893e-04 | 4.4520937e-03 |
# IPC分析
# 参考资料
- LaurensEiroa/Narma10-System-Identification: A system Identification task using a Recurrent Neural Network is performed making use of the Reservoir Computing paradigm. (github.com) (opens new window)
- kubota0130/ipc (github.com) (opens new window)
# Task-dependent IPC
算IPC只能是基于输入信号的延迟的,可以分析具体任务指标与IPC之间的关系吗?比如说话人识别需要哪个类型的IPC?
参考文献:Hülser, T., et al. (2022). "Deriving task specific performance from the information processing capacity of a reservoir computer."
可行性分析:
- 原文中使用了四个一维回归任务,但说话人识别是高维的;
- 原文的输入是需要服从某一分布的,分类任务的输入不能满足;
- 原文表示,“Unifying framework for information processing in stochastically driven dynamical systems”这篇文献可以直接计算NARMA10任务的相关IPC
曲线救国,只对时间序列预测任务NARMA10分析需要的IPC,完善节“IPC对比”
# 记忆容量(MC)
基于RC,Jaeger(2001)通过短期记忆容量(Short-term MC)定义并量化了短时记忆(Short-term Memory),该容量通过计算相关性来衡量网络在网络输出上从储层重建过去信息的能力:
使用可决系数(the determination coefficient)进行计算:

计算流程
- 从标准正态分布中采样,训练输出权重
- 从标准正态分布中采样,计算从零延迟到最大延迟的MC
- 对MC求和
- 一般来说,隐藏权重的谱半径<1;
- 说话人识别任务需要系统有短时记忆的能力吗?MC似乎只适用于ESN计算?
- 迁移至DRC?应该没问题,DRC没有隐藏权重需要定义;迁移至Fit-DNN?只能先训练出输入、隐藏和输出权重,再进行第二步。
- MC与IPC都考察的是信息还原的能力,
参考资料
- Jaeger, H. (2001). Short term memory in echo state networks, GMD Forschungszentrum Informationstechnik.
IPC VS. MC
- IPC量化了储层在衰落记忆函数的希尔伯特空间中重建一组基函数的能力,是线性记忆容量概念的推广;
- IPC = 线性IPC + 非线性IPC;
- 线性IPC(角度2) ≠ Jaeger提出的MC,尽管都使用了相关系数;
- IPC适用于任何动力系统,MC仅针对储油层计算提出,且具有输入-输出的直接连接;
参考资料
# 李雅普诺夫指数(LE)
$$\lambda=\frac{1}{l} \lim _{l \rightarrow \infty} \ln \frac{\gamma_l}{\gamma_0}$$
- 评估初始条件扰动的平均敏感性,$\lambda<0$表示系统属于稳定状态,反之表示混沌状态;
- 向两个一样的系统中分别输入原始信号和加了扰动的信号,$\gamma$表示两个系统状态之间的欧几里得距离,$l$表示时间步;
- 当$\lambda=0$时,系统会发生分岔;
- 对于一维数据,只有一个LE,对于多维数据,我们就有李雅普诺夫谱,但是一般只分析最大LE,因为它代表了
$$\lambda(r)=\lim {n \rightarrow \infty} \frac{1}{n} \sum{i=0}^{n-1} \log \left|\frac{d f_r}{d x}\left(x_i^{(r)}\right)\right|$$
- 这直接就是精确解了?
# Matlab函数
Lyapunov指数的计算方法如下:
lyapunovExponent函数首先生成具有嵌入维数$m$和滞后$τ$的延迟重建$Y_{1:N}$;- 对于一个点$i$,查找最邻近的点$i^$,该点满足$\min _{i^}\left|Y_i-Y_{i^}\right|$,且$\left|i-i^\right|>\text { MinSeparation }$,其中$\text {MinSeparation}$——平均周期——是平均频率的倒数;
- 根据Rosenstein法
资料
- Mathematica有计算示例
- Matlab有个函数
# 参考资料
- 混沌多项式展开法(PCE法)概述 - 知乎 (zhihu.com) (opens new window)
- 随机展开法:PCE Askey方案 - 小张的小跟班 - 博客园 (cnblogs.com) (opens new window)
- 不太确定的话,来个混沌多项式展开吧.py - 知乎 (zhihu.com) (opens new window)
- Software for delay differential equations (kuleuven.be) (opens new window)
- Software | CDLab – Computational Dynamics Laboratory (uniud.it) (opens new window)
Wolf法
- Wolf Lyapunov exponent estimation from a time series. - File Exchange - MATLAB Central (mathworks.cn) (opens new window)
- Calculation Lyapunov Exponents for ODE - File Exchange - MATLAB Central (mathworks.cn) (opens new window)
Rosenstein法
- M.T. Rosenstein, J.J. Collins, C.J. De Luca, A practical method for calculating largest Lyapunov exponents from small data sets, Physica D 65:117-134, 1993.
- sayannag/Lypunov-Exponent-and-Correlation-Dimension: Calculates the largest Lyapunov exponent and the correlation dimension (github.com) (opens new window)
- Topu-Hstu/pyeeg (github.com) (opens new window)
- iank/lyapunov_estimation: Estimate maximum Lyapunov exponent for short time series using Rosenstein, et al. method (github.com) (opens new window)
- Largest Lyapunov Exponent with Rosenstein's Algorithm - File Exchange - MATLAB Central (mathworks.cn) (opens new window)
机器学习替代模型
- Model-Free Prediction of Large Spatiotemporally Chaotic Systems from Data: A Reservoir Computing Approach
- Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data
